Рассмотрим задачу определения потока, заданной величины 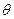 от s к t в сети
от s к t в сети 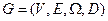 , в которой каждая дуга (xi,xj) характеризуется пропускной способностью
, в которой каждая дуга (xi,xj) характеризуется пропускной способностью 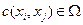 и неотрицательной стоимостью
и неотрицательной стоимостью 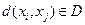 пересылки единичного потока из xi в xj вдоль дуги (xi,xj).
пересылки единичного потока из xi в xj вдоль дуги (xi,xj).
Если 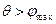 , где
, где 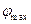 - величина максимального потока в сети G от s к t, то решения нет. Если же
- величина максимального потока в сети G от s к t, то решения нет. Если же 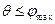 , то может быть определено несколько различных потоков величины
, то может быть определено несколько различных потоков величины 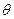 от s к t.
от s к t.
Математическая модель задачи выглядит следующим образом: минимизировать 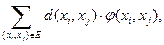 где
где 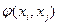 - поток по дуге (xi,xj) при ограничениях:
- поток по дуге (xi,xj) при ограничениях:
1. 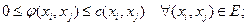
2. Для начальной вершины 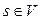 :
: 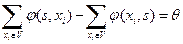 - уравнение истока;
- уравнение истока;
3. Для конечной вершины 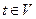 :
: 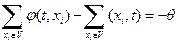 - уравнение стока;
- уравнение стока;
4. Для любой другой вершины xj≠s, t: 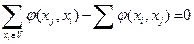 - условие сохранения потока.
- условие сохранения потока.
Если µ* - кратчайший путь от s к t в сети G=(V,E,D), cmin(µ*) – минимальная из пропускных способностей дуг, входящих в путь µ*, и если 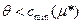 , то задача имеет тривиальное решение – весь поток
, то задача имеет тривиальное решение – весь поток 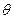 направляется вдоль пути µ*.
направляется вдоль пути µ*.
Общее решение задачи о потоке минимальной стоимости строится следующим образом. Сначала находится кратчайший путь µ* от s к t и величина 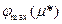 максимально возможного потока вдоль этого пути. Если окажется, что
максимально возможного потока вдоль этого пути. Если окажется, что 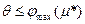 , то задача решена. В противном случае сеть модифицируют специальным образом. Затем опять находят кратчайший путь от s к t и максимально возможный поток вдоль этого пути в модифицированной сети. Процедуры модификации сети и нахождения пути в ней повторяются до тех пор, пока либо нужное количество
, то задача решена. В противном случае сеть модифицируют специальным образом. Затем опять находят кратчайший путь от s к t и максимально возможный поток вдоль этого пути в модифицированной сети. Процедуры модификации сети и нахождения пути в ней повторяются до тех пор, пока либо нужное количество 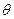 не будет переправлено, либо возникнет сеть, в которой нет пути от s к t, что означает отсутствие решения у исходной задачи.
не будет переправлено, либо возникнет сеть, в которой нет пути от s к t, что означает отсутствие решения у исходной задачи.
Модифицированная относительно данного потока 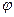 сеть
сеть 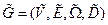 строится следующим образом:
строится следующим образом:
1. 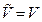 , т.е. число и набор вершин в модифицированной сети не изменяется.
, т.е. число и набор вершин в модифицированной сети не изменяется.
2. 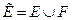 , где F – некоторое множество фиктивных дуг. Т.о., после модификации число дуг сети увеличивается.
, где F – некоторое множество фиктивных дуг. Т.о., после модификации число дуг сети увеличивается.
3. Если 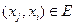 и
и 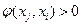 , то (xi,xj) включается в множество F. При этом полагается
, то (xi,xj) включается в множество F. При этом полагается 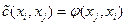 ,
, 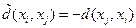 . Этот пункт применяется только к дугам, по которым проходит поток
. Этот пункт применяется только к дугам, по которым проходит поток 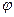 , относительно которого происходит модификация сети.
, относительно которого происходит модификация сети.
4. Для всех ненасыщенных дуг, где нет противоположного потока, в том числе и для ненасыщенных дуг с потоком, относительно которого происходит модификация сети, т.е. для 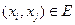 ,
, 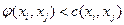 и
и 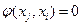 полагают
полагают 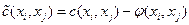 ,
, 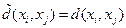 .
.
5. Для всех насыщенных дуг 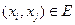 ,
, 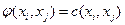 и
и 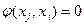 , полагают
, полагают 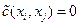 ,
, 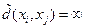 .
.
 2015-07-03
2015-07-03 220
220






