Транспортные задачи линейного программирования

1. Определение транспортной модели.

2. Сбалансированная транспортная модель.

3. Метод потенциалов.

4. Пример решения транспортной задачи.

5. Дополнительные ограничения в задачах транспортного типа.

6. Транспортная задача в сетевой постановке.

7. Доставка груза в кратчайший срок.

Симплекс-метод дает возможность решить любую задачу линейного программирования. Однако существует много методов, которые учитывают конкретные особенности каждой из этих задач, а потому более эффективных. К числу таких задач относятся транспортные задачи.

Под термином "транспортные задачи" понимается широкий круг задач не только транспортного характера. Общим для них является, как правило, распределение ресурсов, находящихся у m производителей (поставщиков), по n потребителям этих ресурсов.

Транспортная задача (ТЗ) является важнейшей частной задачей линейного программирования, имеющей обширные практические приложения не только к проблемам транспорта. Она выделяется в линейном программировании определённостью экономической характеристики, особенностями математической модели, наличием специфических методов решения.

К ЗЛП транспортного типа приходят при рассмотрении различных практических ситуаций, связанных с составлением наиболее экономичного плана перевозок продукции, управления запасами, назначением персонала на рабочие места, оборотом наличного капитала и многими другими.

На транспорте наиболее часто встречаются следующие задачи, относящиеся к транспортным:

- прикрепление потребителей ресурса к производителям;

- привязка пунктов отправления к пунктам назначения;

- взаимная привязка грузопотоков прямого и обратного направлений;

- отдельные задачи оптимальной загрузки промышленного оборудования;

- оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др.

На рис. 1.11 показано общее представление транспортной задачи в виде сети с m пунктами отправления и n пунктами назначения, которые показаны в виде узлов сети. Дуги, соединяющие узлы сети, соответствуют маршрутам, связывающим пункты отправления и назначения. С дугой (i, j), соединяющей пункт отправления i с пунктом назначения j, соотносятся два вида данных: стоимость c_ij перевозки единицы груза из пункта i в пункт j и количество перевозимого груза x_ij. Объем грузов в пункте отправления i равен а_i, а объем грузов в пункте назначения j - b_j. Задача состоит в определении неизвестных величин х_ij минимизирующих суммарные транспортные расходы и удовлетворяющих ограничениям, налагаемым на объемы грузов в пунктах отправления (предложения) и пунктах назначения (спрос).

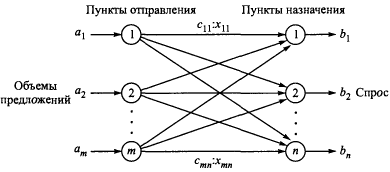
Рис. 1.11. Представление транспортной задачи

Рассмотрим экономико-математическую модель прикрепления пунктов отправления к пунктам назначения. Имеются m пунктов отправления груза A₁, A₂, A_m и объемы отправления по каждому пункту а₁, a₂, a_m. Известна потребность в грузах b₁, b₂, b_n по каждому из n пунктов назначения B₁, B₂, B_n. Задана матрица стоимостей доставки по каждому варианту с_ij, i = 1, 2, m; j = 1, 2, n. Необходимо рассчитать оптимальный план перевозок, т. е. определить, сколько груза должно быть отправлено из каждого A_i-го пункта отправления (от поставщика) в каждый B_j-й пункт назначения (до потребителя) х_ij с минимальными транспортными издержками.

В общем виде исходные данные транспортной задачи представлены в табл. 1.8.

Таблица 1. 8. Транспортная таблица

	В1	В2	…	Вn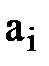
А1	x11	c11	x12	c12	…	x1n	c1n	а1
А2	x21	c21	x22	c22	…	x2n	c2n	а2
…	…		…		…	…		…
Аm	xm1	cm1	xm2	cm2	…	xmn	cmn	аm
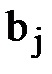	b1	b2	…	bn

Тогда математическая модель транспортной задачи формулируется следующим образом:

(7.1)

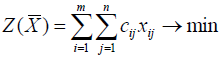
при ограничениях

(7.3)

(7.2)

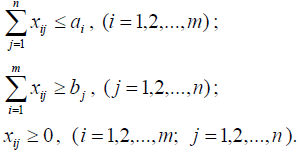
Первое ограничение означают, что суммарный объем перевозок от i -го поставщика не может превышать имеющегося у него запаса товара a_i. Второе ограничение означают, что суммарные перевозки товара j-му потребителю должны полностью удовлетворить его потребности в товаре b_j. Третье ограничение исключает обратные перевозки.

Из первых двух ограничений следует, что:

(7.4)

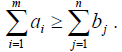
Если имеет место равенство

(7.5)

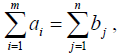
то модель называется сбалансированной транспортной моделью. В сбалансированной модели первые два ограничения имеют вид равенств. В реальных условиях запас товара не всегда равен спросу (потребности), но транспортную модель всегда можно сбалансировать.

В случае превышения запаса над спросом, т.е. если

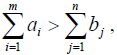
то вводится фиктивный (n + 1) -й потребитель со спросом

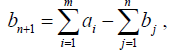
а соответствующие стоимости с_i,n+1 (i = 1,2, m) считаются равными нулю.

Аналогично, при

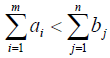
вводится фиктивный (m +1) -й поставщик с запасом товара

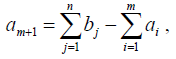
а соответствующие стоимости с_{m + 1,j} (j = 1,2, n) считаются равными нулю.

Таким образом, исходная задача сводится к сбалансированной транспортной задачи, из оптимального плана которой получается оптимальный план несбалансированной транспортной задачи.

Отметим, несбалансированную транспортную задачу называют также открытой транспортной задачей, тогда как сбалансированную транспортную задачу - закрытой транспортной задачей. Стремление сбалансировать транспортную задачу обусловлено возможностью применить в этом случае эффективный вычислительный метод.

Наиболее распространенным методом решения транспортных задач является метод потенциалов, который был предложен в 1949 г. советскими математиками Л.В. Канторовичем и М.К. Гавуриным. Позже аналогичный метод разработал американский математик Дж. Данциг, основываясь на общих идеях линейного программирования.

Решение задачи методом потенциалов включает следующие этапы:

- разработку начального плана (опорного решения);

- расчет потенциалов;

- проверку плана на оптимальность;

- поиск максимального звена неоптимальности (если полученный план не оптимальный);

- составление контура перераспределения ресурсов;

- определение минимального элемента в контуре перераспределения и перераспределение ресурсов по контуру;

- получение нового плана.

Описанный алгоритм является итерационным и выполняется до тех пор, пока не будет найдено оптимальное решение.

Число неизвестных переменных x_ij в транспортной задаче с m поставщиками и n потребителями равно m× n, а число уравнений в системе (7.2) - (7.3) равно m+n. Так как транспортная задача является сбалансированной, т.е. выполняется условие (7.5), то число линейно независимых уравнений равно m+n-1. Следовательно, опорный план транспортной задачи может иметь не более m+n-1 отличных от нуля неизвестных. Если данное условие не выполняется, то план называется вырожденным.

Для транспортной задачи существует несколько методов отыскания начального плана (опорного решения): метод северо-западного угла; метод минимальной стоимости; метод Фогеля и т. д.

Различие этих методов заключается в "качестве" начального решения, т.е. "удаленности" начального решения от оптимального. В общем случае метод Фогеля, предложенный американским ученым, дает наилучшее решение, а метод северо-западного угла – наихудшее. Однако метод северо-западного угла требует меньшего объема вычислений.

Вычислительный алгоритм метода потенциалов рассмотрим на примере решения конкретной задачи прикрепления трех пунктов отправления (поставщиков) i = 1, 2, 3 к четырем пунктам назначения (потребители) j = 1, 2, 4 в соответствии с исходными данными табл. 1.9.

Таблица 1.9. Исходные данные

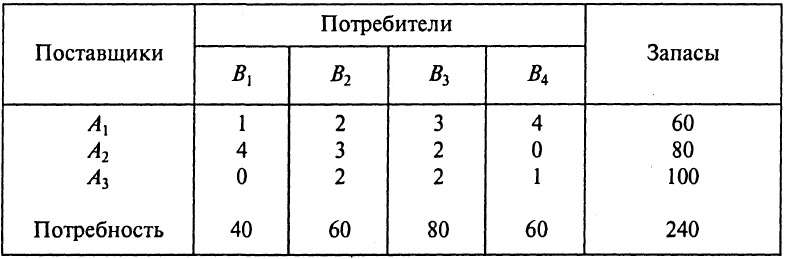
Начальный план можно составить одним из перечисленных выше методов. Воспользуемся наиболее простым методом – методом северо-западного угла. В соответствии с этим методом загрузка клеток (определение базисных переменных по распределению объемов пунктов отправления к пунктам назначения) начинается с верхней левой клетки («северо-западная» часть таблицы) и продолжается вниз и вправо (по диагонали).

По указанному правилу загружаем первую клетку на основе следующего условия: х₁₁ = min {а₁; b₁} = min {60; 40} = 40.

Таким образом, первый пункт назначения загружен, а первый пункт отправления имеет остатки груза Da₁ = 60-40 = 20, которые и распределяем на второй пункт назначения: x₁₂ = min {Da₁; b₂} = min {20; 60} = 20; Db₂ = 40.

Продолжая преобразования аналогичным образом, получаем: x₂₂ = min {a₂; Db₂} = min {80; 40} = 40; Da₂ = 40 и т д. Процесс продолжается до тех пор, пока не будут удовлетворены все потребители за счет запасов поставщиков.

Результаты начального плана и расчета потенциалов представлены в табл. 1.10.

В процессе решения после каждой итерации (в том числе и после получения допустимого решения) по числу загруженных клеток проверяется опорный план на вырожденность, т.е. число загруженных клеток должно быть не больше числа уравнений: N = m + n – 1 = 4 + 3-1 = 6.

Таблица 1.10. Начальный план перевозок

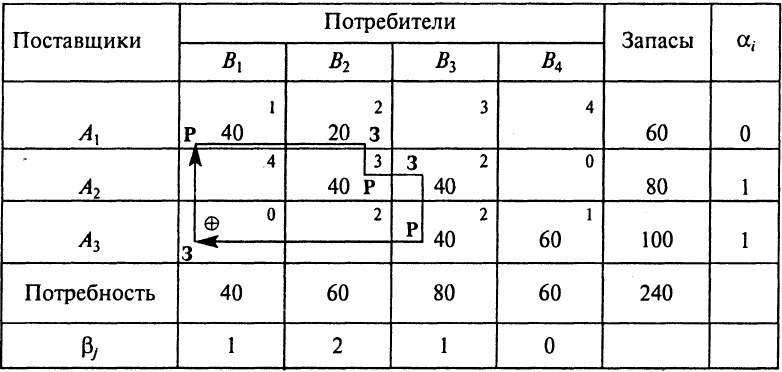
В том случае, если число загруженных клеток меньше числа уравнений, то нужно в любые свободные клетки поставить нули. Клетка, в которой стоит ноль, считается занятой.

Значение целевой функции по результатам расчета допустимого плана:

Z₀ = 1 × 40 + 2 × 20 + 3 × 40 + 2 × 40 + 2 × 40 + 1 × 60 = 420.

Расчет потенциалов выполняют по загруженным клеткам, для которых должно выполняться следующее равенство:

α_i + β_j = с_ij, (7.6)

где α_i потенциал поставщика А_i, который записывают в новом столбце справа от таблицы; βj потенциал потребителя В_j, который записывают в новой строке под таблицей. Данные потенциалы выбирают так, чтобы в любой базисной клетке их сумма равнялась тарифу, т.е. выполнялось равенство (7.6). Так как количество всех потенциалов α_i и β_j составляет m + n, а занятых клеток m + n - 1, то для определения чисел α_i и β_j придется решать систему из m + n - 1 уравнений с m + n неизвестными. Поэтому одному из неизвестных потенциалов придают произвольное значение (например, нулевое). Тогда остальные значения определяются однозначно.

Вычисляя потенциалы по выражению (7.6), принимаем для первой строки α_i = 0. Используя загруженные клетки (i–j) = (1–1), (1–2), получаем:

α₁ + β₁ = с₁₁ = 0 + β₁ = 1, β₁ = 1;

α₁ + β₂ = с₁₂ = 0 + β₂ = 2, β₂ = 2.

Далее по загруженным клеткам (2–2), (2–3) определяем другие потенциалы:

α₂ + β₂ = 3, α₂ + 2 = 3, α₂ = 1;

α₂ + β₃ = 2, 1 + β₃ = 2, β₃ = 1.

Результаты расчета потенциалов для опорного плана представлены в табл. 1.10.

Для проверки оптимальности плана просматривают свободные клетки, для которых определяют оценки Dс_ij – разность между тарифом клетки и суммой потенциалов строки и столбца, т.е. Dс_ij = c_ij-(α_i + β_j). Экономически оценка Dс_ij показывает, размер экономии транспортных издержек на 1 ед. перевозимого груза. Если все оценки неотрицательные, т.е. Dс_ij ≥ 0 или α_i + β_j ≤ с_ij, (7.7) то план оптимальный и остается подсчитать транспортные расходы.

По табл. 1.10 осуществляем проверку начального плана на оптимальность:

- (i–j) = (1–3), 0 + 1 ≤3;

- (i–j) = (1–4), 0 + 0 ≤ 4;

- (i–j) = (2–1), 1 + 1 ≤ 4;

- (i–j) = (2–4), 1 + 0 > 0, Dс₂₄ = -1;

- (i–j) = (3–1), 1 + 1 > 0, Dс₃₁ = -2;

- (i–j) = (3–2), 1 + 2 > 2, Dс₃₂ = -1.

Итак, по трем клеткам условие (7.7) не выполняется, следовательно, начальный план требует улучшения. Наибольшую экономию можно получить по клетке (i–j) = (3–1), где Dс₃₁ = -2, так как данное значение больше по абсолютной величине других оценок {Dс₂₄ = -1; Dс₃₂ = -1}. Следовательно, клетку (3-1) необходимо загрузить за счет перераспределения ресурсов из других загруженных клеток. В табл. 1.10 клетку (3–1) помечаем знаком «+», так как здесь в начальном плане находится вершина максимальной неоптимальности.

Контур перераспределения ресурсов составляют по следующим правилам:

- этот контур представляет замкнутый многоугольник с вершинами в загруженных клетках, за исключением клетки с вершиной максимальной неоптимальности «+», и звеньями, лежащими вдоль строк и столбцов матрицы;

- ломаная линия должна быть связанной в том смысле, что из любой ее вершины можно попасть в любую другую вершину по звеньям ломаной цепи (по строке или по столбцу);

- в каждой вершине контура встречаются только два звена, одно из них располагается по строке, другое – по столбцу;

- число вершин контура четное, все они в процессе перераспределения делятся на загружаемые (З) и разгружаемые (Р);

- в каждой строке (столбце) имеются две вершины: одна – загружаемая, другая –разгружаемая.

В клетке максимальной неотимальности намечаем одну из вершин контура и далее по вышеизложенным правилам строим контур, вершины которого будут находиться в клетках (3–1) – (1–1) – (1–2) – (2–2) – (2-3) – (3–3). Вершины контура последовательно подразделяем на загружаемые (3) и разгружаемые (Р), начиная с вершины максимальной неоптимальности «+» (табл. 1.10).

Перераспределение ресурсов по контуру осуществляется с целью получения оптимального плана. В процессе перераспределения ресурсов по контуру в соответствии с условием неотрицательности переменных х_ij ни одно из этих значений не должно превратиться в отрицательное число. Поэтому анализируют только клетки, помеченные знаком Р, из которых выбирают клетку с минимальным объемом перевозок. В нашем примере Xmin = min{40; 40; 40} = 40. Следовательно, клетки (1–1), (2–2), (3–3) полностью разгружаются. В клетке (1–2) загрузка увеличится на 40 и достигнет 60, в клетке (2–3) загрузка составит 40 + 40 = 80, и клетка (3–1) загрузится на 40 (табл. 1.11).

Таблица 1.11. Первый план перевозок

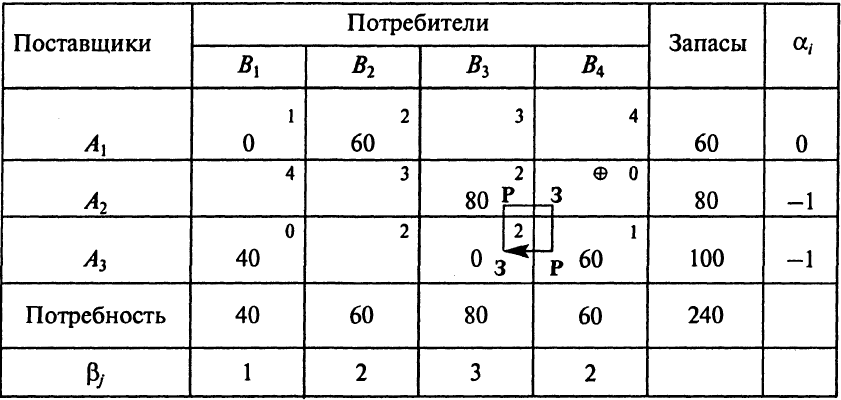
Проверяем условие не вырожденности число уравнений N = m + n - 1 должно быть ровно количеству переменных (числу загруженных клеток). Внашем примере m = 3, n = 4, а число загруженных клеток равно 4, т. е. условие не выполняется и 6 ≠ 4. В процессе перераспределения ресурсов произошла полная разгрузка трех клеток, а должна освободиться только одна клетка. В этом случае следует в две клетки проставить нули (нулевой ресурс) и считать условно их загруженными. Например, в клетки (1–1) и (3–3) проставим нулевой ресурс (рис. 1.11).

По результатам первой итерации имеем:

Z₁ = 2 × 60 + 2 × 80 + 1 × 60 + 0 × 40 = 340.

Получение очередного плана (итерации) осуществляется в том же порядке, который был рассмотрен выше, т. е.:

- по загруженным клеткам (в соответствии с новой загрузкой) вычисляются потенциалы αi и βj;

- по незагруженным клеткам производится проверка плана на оптимальность;

- находится вершина максимальной неоптимальности и строится новый контур перераспределения и т. д., до тех пор, пока не будет найдено оптимальное решение, удовлетворяющее неравенству (7.7).

Ниже приведены расчеты по второй итерации. Поиск потенциалов для первого плана следующий:

α₁ + β₁ = 1,0 + β₁ = 1, β₁ = 1;

α₁ + β₂ = 2, 0 + β₂ = 2, β₂ = 2;

α₃ + β₁ = 0, α₃ + 1 = 0, α₃ = -1;

α₃ + β₃ = 2, -1 + β₃ = 2, β₃ = 3;

α₂ + β₃ = 1, α₂ + 3 = 2, α₂ = -1;

α₃ + β₄ = 1, -1 + β₄ = 1, β₄ = 2.

Проведем проверку на оптимальность первого плана:

(i–j) = (1–3), 0+3 ≤ 3;

(i–j) = (1–4), 0+4 < 4;

(i–j) = (2–1), -1+1 < 4;

(i–j) = (2–2), -1+2 < 3;

(i–j) = (3–2), -1+2 < 2;

(i–j) = (2–4), -1+2 > 0.

Клетку (2–4) необходимо загрузить. В соответствии с перераспределением ресурсов по контуру получаем табл. 1.12, для которой вновь рассчитываем потенциалы α_i и β_j, и последовательность вычислений повторяется.

Таблица 1.12. Оптимальный план перевозок

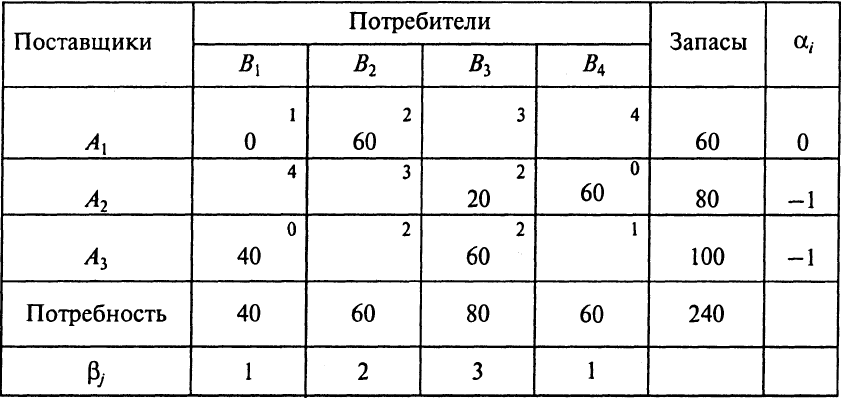
Для распределения, полученного в табл. 1.12, условие (7.7) выполняется, следовательно, план – оптимальный.

Транспортные издержки по оптимальному плану следующие:

Z₂ = 1 × 0 + 2 × 60 + 2 × 20 + 0 × 60 + 0 × 40 + 2 × 60 = 280.

Таким образом, построением начального плана с последующим расчетом двух итераций получено оптимальное решение по прикреплению пунктов отправления грузов к пунктам назначения. Однако рассмотренная задача является классической транспортной задачей и в экономике предприятия такие задачи встречаются крайне редко. Обычно при составлении экономико-математической модели в задачи транспортного типа приходится вводить целый ряд дополнительных ограничений, а затем ее решать методом потенциалов.

Рассмотрим наиболее часто встречающиеся ситуации в экономике предприятия.

1. Отдельные поставки от определенных поставщиков некоторым потребителям должны быть исключены (из-за отсутствия необходимых условий хранения, чрезмерной перегрузки коммуникаций и т. д.). Это ограничение требует, чтобы в матрице перевозок, содержащей оптимальный план, определенные клетки оставались свободными. Последнее достигается искусственным завышением затрат на перевозки с_ij в клетках, перевозки через которые следует запретить. При этом производят завышение величины с_ij до таких значений, которые будут заведомо больше всех, с которыми их придется сравнивать в процессе решения задачи.

2. На предприятии необходимо определить минимальные суммарные затраты на производство и транспортировку продукции. С подобной задачей сталкиваются при решении вопросов, связанных с оптимальным размещением производственных объектов. Здесь может оказаться экономически более выгодным доставлять сырье из более отдаленных пунктов, но зато при меньшей его себестоимости. В таких задачах за критерий оптимальности принимают сумму затрат на производство и транспортировку продукции.

3. Ряд транспортных маршрутов, по которым необходимо доставить грузы, имеют ограничения по пропускной способности. Если, например, по маршруту A_i – B_j можно провести не более q единиц груза, то B_j столбец матрицы разбивается на два столбца – B'_j и B''_j. В первом столбце спрос принимается равным разности между действительным спросом b_j и ограничением q: b'_j = b_j-q, во втором – равным ограничению q, т. е. b''_j = q. Затраты с_ij в клетке второго столбца равны данным, но в клетке первого столбца вместо истинного тарифа с_ij ставится искусственно завышенный тариф М (клетка блокируется). Затем задача решается обычным способом.

4. Поставки по определенным маршрутам обязательны и должны войти в оптимальный план независимо от того, выгодно это или нет. В этом случае уменьшают запас груза у поставщиков и спрос потребителей и решают задачу относительно тех поставок, которые необязательны. Полученное решение корректируют с учетом обязательных поставок.

5. Экономическая задача не является транспортной, но в математическом отношении подобна транспортной, так как описывается аналогичной моделью, например распределение производства изделий между предприятиями, оптимальное закрепление механизмов по определенным видам работы.

6. Необходимо максимизировать целевую функцию задачи транспортного типа. В этой ситуации при составлении опорного плана в первую очередь стараются заполнить клетки с наиболее высокими значениями показателей с_ij. Выбор клетки, подлежащей заполнению при переходе от одного допустимого плана к другому, должен производиться не по минимальной отрицательной разнице [с_ij-(α_i + β_j)], а по максимальной этой разнице. Оптимальным будет план, которому в последней таблице сопутствуют свободные клетки с неположительными элементами: все разности [с_ij -(α_i + β_j)] ≤ 0.

7. Необходимо в одно время распределить груз различного рода по потребителям. Задачи данного типа называются многопродуктовыми транспортными задачами. В этих задачах поставщики m родов грузов разбиваются на m условных поставщиков, а потребители n родов грузов разбиваются на n условных потребителей. С учетом этой разбивки составляют полную транспортную таблицу. При этом заметим, что некоторые маршруты A_iB_j должны быть блокированы (закрыты), поскольку в данной постановке задачи грузы разного рода не могут заменять друг друга.

Этим маршрутам A_iB_j должна соответствовать очень высокая стоимость перевозки. Многопродуктовую задачу не всегда обязательно описывать одной моделью. Например, если поставки грузов различного рода независимы, то задачу можно представить в виде комплекса транспортных задач по каждому роду груза. Однако, если между грузами различного рода существует связь (например, одни из грузов можно заменить другими), то в общем случае исходную модель (задачу) не удается разбить на комплекс простых транспортных задач.

В практической деятельности могут возникнуть ситуации, когда нас в первую очередь интересуют не затраты на перевозку груза (их минимизация), а время доставки этих грузов потребителям. Например, при подготовке крупных военных операций, когда необходимо в кратчайший срок сосредоточить ресурсы в намеченных пунктах или при стихийных бедствиях (землетрясение, ураганы и т. п.), возникает задача обеспечения пострадавших районов различными ресурсами в кратчайший срок.

Для решения подобных задач рассмотренный ранее метод потенциалов непригоден. Эти задачи решаются с помощью специального алгоритм. Смысл этих алгоритмом состоит в построении любым способом опорного плана построении разгрузочных циклов для клеток транспортной таблицы с критическим временем перевозки.

Если условия транспортной задачи заданы в виде схемы, на которой условно изображены поставщики, потребители и связывающие их дороги, указаны величины запасов груза и потребности в нем, а также транспортные издержки по доставке грузов, то говорят, что транспортная задача поставлена в сетевой форме.

В таких задачах сетевой формы пункты расположения поставщиков и потребителей изображают вершинами (узлами) сети, запасы груза записывать в вершинах положительными, а потребности – отрицательными числами. Дороги, связывающие пункты расположения и потребления груза, изображают линиями и называют ребрами (дугами, звеньями) сети.

Различия между транспортными задачами в матричной и сетевой формах весьма незначительны, так как методы решения их основаны на одних и тех же идеях (метод потенциалов).

Литература

1. Бережная Е. В. Математические методы моделирования экономических систем: учеб. пособие. – 2-е изд., перераб. и доп. / Е. В. Бережная, В. И. Бережной. – М.: Финансы и статистика, 2006. – 432 с.

2. Стариков А. В. Экономико-математическое и компьютерное моделирование [Текст]: учеб. пособие / А. В. Стариков, И. С. Кущева; Фед. агентство по образованию, ГОУ ВПО «ВГЛТА». – Воронеж, 2008. – 132 с.

3. Большакова И.В. Линейное программирование: учебно-метод. пособие к контрольной работе для студ. эконом. факультета / И.В. Большакова, М.В. Кураленко. – Мн.: БНТУ. 2004. – 148 с.

4. Таха Хемди А. Введение в исследование операций, 7-е издание: пер. с англ. – М.: Издательский дом "Вильяме", 2005. – 912 с.

5. Грешилов А.А. Прикладные задачи математического программирования: учебное пособие. – 2-е изд. – М.: Логос, 2006. – 288 с.