Пример описания транспортной задачи для оптимизации системы товародвижения

В системе товародвижения очень важную роль играет транспорт. Большая доля затрат в товародвижении приходится именно на транспортные перевозки. Следовательно необходимо искать пути снижения этих затрат, например с помощью маршрутизации, оптимизации процессов сопутствующих перевозкам, а также с помощью математических методов и т.п. Среди математических методов наиболее разработаны методы линейного программирования. Слово «линейное» определяет математическую сущность метода, которая заключается в том, что с его помощью решаются задачи с линейными связями и ограничениями, т.е. если выразить задачу в математической форме, то в ней все неизвестные будут в первой степени.

На автомобильном транспорте методом линейного программирования решают такие задачи:

· отыскание оптимального числа ездок автомобилей на маршрутах при установленном времени пребывания в наряде (задача на минимальные потери рабочего времени);

· отыскание оптимального варианта закрепления получателей за поставщиками однородной продукции (задача на минимум нулевых пробегов);

· составление рациональных маршрутов работы подвижного состава – увязка ездок (задача на минимум холостых пробегов);

· организация развозочных и сборочных маршрутов (задача на определение минимального пробега при объезде грузопунктов);

· распределение подвижного состава и погрузочно-разгрузочных средств по маршрутам работы (задача на максимальное использование рабочего времени автомобилей и погрузочно-разгрузочных механизмов и др.).

Все перечисленные задачи базируются на математическом моделировании изучаемого процесса, т.е. описании количественных закономерностей этого процесса с помощью математических выражений (математической модели). Математическая модель является абстрактным изображением реального процесса и в меру своей абстрактности может его характеризовать более или менее точно.

Применительно к ВМЗ рассмотрим решение транспортной задачи, для отыскания оптимального прикрепления потребителей (розничных магазинов) к региональным складам дилеров занимающихся продажей газовых плит ВМЗ, расположенных в липецкой и белгородской областях.

Постановка задачи. Имеется m поставщиков, располагающих определенным количеством продукции, и n потребителей, у которых есть потребность на данную продукцию. Известны транспортные расходы по доставке единицы продукции от любого поставщика до любого потребителя. Требуется прикрепить потребителей к поставщикам так, чтобы суммарные транспортные расходы по доставке всей продукции потребителям были минимальными.

Для построения экономико-математической модели введем обозначения:

i – номер (индекс) поставщика (i = 1, 2,..., m); пусть m = 4, т.е. имеются четыре поставщика (i = 1, 2, 3, 4);

А_i – ресурсы i-го поставщика (i = 1, 2, 3, 4), т.е. количество продукции, которое поставщик может отправить потреби­телям; пусть A₁ = 160 шт., A₂ = 240 шт., А₃ = 100 шт., А₄ = 200 т, а всего — 700 шт.;

j – номер (индекс) потребителя (j = 1, 2,..., n); пусть n = 5, тогда (j= 1, 2, 3, 4, 5);

В_j – потребность в продукции j-го потребителя; пусть В₁ = 150 шт.,

В₂ =180 шт., В₃ = 200 шт., В₄ = 120 шт., В₅ = 50 шт., а всего – 700 шт.;

C_ij — транспортные расходы по доставке единицы продукции от i-го поставщика j-му потребителю. Пусть транспортные расходы для числового примера заданы в таблице 1;

X_ij – количество продукции, поставляемое от i-го поставщика j-му потребителю; эта величина неизвестна и подлежит определению; в процессе решения задачи должны быть найдены все значения Х_ij, указанные в таблице 2.

Таблица 1

Транспортные расходы по доставке единицы продукции i – го поставщика j – му потребителю

Потребители Поставщики	j =1	j = 2	j = 3	j = 4	j = 5
i = 1	С11 = 2	С12 = 6	С13 = 4	С14 = 10	С15 = 4
i = 2	С21 = 7	С22 = 5	С23 = 2	С24 = 7	С25 =10
i = 3	С31 = 5	С32 = 2	С33 = 6	С34 = 5	С35 = 9
i = 4	C41 = 3	С42 = 9	С43 = 4	С44 = 4	С45 = 4

Таблица 2

Матрица решений

Потребители Поставщики	j =1	j = 2	j = 3	j = 4	j = 5
i = 1	X11 Xij	X12 …	X13 …	X14 …	X15 Xij
i = 2	X21 Xij	X22 …	X23 …	X24 …	X25 Xij
i = 3	X31 Xij	X32 …	X33 …	X34 …	X35 Xij
I = 4	X41 Xij	X42 …	X43 …	X44 …	X45 Xij

Составим таблицу 3, в которую сведем исходные данные для решения экономико-математической модели: ресурсы поставщиков, потребности потребителей и тран­спортные расходы (они проставлены в выделенных прямоугольни­ках). Кроме того, в таблице 3 предусмотрен столбец для записи потенциалов U_i и V_j.

Таблица 3

Исходные данные для оптимального решения прикрепления потребителей к поставщикам

	Потребители	j = 1	j = 2	j = 3	j = 4	j = 5	Ресурсы поставщиков
Поставщики	Vj	V1	V2	V3	V4	V5
Ui
i = 1	U1	X11	X12	X13	X14	X15
i = 2	U2	X21	X22	X23	X24	X25
i = 3	U3	X31	X32	X33	X34	X35
i = 4	U4	X41	X42	X43	X44	X45
Потребности потребителей

Построение модели. Экономико-математическая модель оптимального прикрепления содержит целевую функцию, системы ограничений (определенные условия) и условия неотрица­тельности переменных.

В рассматриваемой модели ставится задача свести к минимуму транспортные расходы.

Для нашего числового примера целевая функция будет иметь вид:

2X₁₁ + 6X₁₂+ 4X_13… X₂₁+X₂₂ +…X₄₅ = min

В общем виде целевая функция выглядит так:

C₁₁X₁₁+C₁₂X₁₂+…+C₃₁X₃₁+C₃₄X₃₄+…+C_mnX_mn = min,

Или

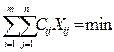
Достижение минимального значения целевой функции должно происходить при определенных условиях. Первое из них состоит в том, что по оптимальному варианту от каждого поставщика плани­ровалось к поставке то количества продукции, которым он распо­лагает. Это условие для рассматриваемого примера записывается в виде системы уравнений.

В общем виде система уравнений для первого условия записывается так:

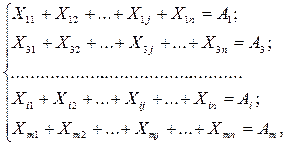
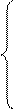или

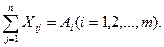
Для нашего числового примера (см. табл. 3)

X11+X12+…+Xj1+…+Xn1 = B1; X31+X32+…+X3j+…+X3n = B3; ………………………………….. X1j+X2j+…+Xij+…+Xmj = Bi; X1n+X2n+…+Xin+…+Xmn = Bn,

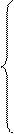Второе условие предусматривает поставку каждому потребителю продукции в пределах потребности.

В общем виде система уравнений для второго условия

записывается так:

или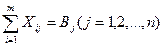

Для нашего числового примера (см. табл. 3)

Xij > 0, т.е. значение переменной (по­ставки) должно быть рав

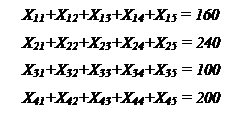но или больше нуля (отрицательное значе­ние поставки не имеет смысла, например, минус 20 т металла).

Таким образом, экономико-математическая модель опти­мального прикрепления потребителей к поставщикам будет иметь следующий вид:

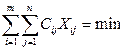
при условиях:

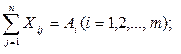
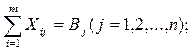
X_ij ³ 0 (I = 1, 2, …,m), (j = 1, 2, …,n).

Приведенная модель является закрытой, т.к.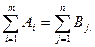

Далее решаем задачу прикрепления поставщиков к потребителям. Расчеты выполняют в специальной таблице (матрице) линейного про­граммирования методом потенциалов. В этой табли­це имеются столбец и строка для записи потенциалов U_i и U_j, которые дают возможность определить оп­тимальность плана закрепления поставщиков за потребителями.

Решение задачи начинается с построения ис­ходного плана.

Метод потенциалов, как и другие методы линейного програм­мирования, требует, чтобы исходный вариант и все последующие варианты удовлетворяли условиям:

1) число загруженных клеток Х_ij в таблице должно быть на единицу меньше суммы чисел поставщиков (m) и числа потребителей (n), в нашем примере это число должно быть равно 8, т.е. m + n - 1 = 4 + 5 – 1 = 8;

2) не должно быть ни одного занятого квадрата, который оказался бы единственным в строке и в столбце таблицы;

3) занятые квадраты таблицы должны быть расположены так, чтобы можно было образовать так называемую вычеркиваемую систему.

Для составления исходного плана воспользуемся приемом, кото­рый называется методом северо-западного угла». Заполнение таблицы прикрепления начинают с левого верхнего квадрата и с позиции этого квадрата сравнивают ресурсы пер­вого поставщика (160 шт.) и потребности первого потребителя (150 шт.), выбрать меньшее значение из них и записать в данный квадрат, ко­торый с этого момента становится «загруженным».

В нашем примере записано значение «150», равное потребности первого потребителя. Затем необходимо подвинуться вправо от се­веро-западного угла и сравнить оставшиеся ресурсы первого по­ставщика (160 - 150 = 10) и потребность второго потребителя (180), записываем наименьшую цифру (10) в квадрат первой строки вто­рого столбца и перемещаемся вниз. Сравниваем неудовлетворенную потребность второго потребителя (180 –10 + 70). Ресурсы второго поставщика составляют (170 + 70 = 240) и т.д.

Так, двигаясь шаг за шагом, получаем исходный план (см. табл. 4). Определим значение некоторых цифр, содержащихся в таблице 4. Числа, выделенные в таблице, - это количество про­дукции, которое по исходному плану намечено к поставке. Квадра­ты, в которых расположены эти цифры, называются «загруженны­ми»; квадраты, не содержащие поставок, — «свободными». /21/

Таблица 4

Исходный план прикрепления потребителей к

поставщикам

	Потребители	j = 1	j = 2	j = 3	j = 4	j = 5	Ресурсы поставщиков
Поставщики	Vj	V1=2	V2=6	V3=3	V4=3	V5=3
Ui
i = 1	U1=0
i = 2	U2= -1
i = 3	U3=3
i = 4	U4=1
Потребности потребителей

Числа, расположенные в свободных квадратах таблицы, явля­ются вспомогательными и представляют собой сумму соответст­вующих условных величин U_i + V_j = С_ij (потенциалов). Для загру­женных квадратов суммы Ui+V_j должны совпадать с транспорт­ными издержками С_ij.

После составления исходного плана проверим условие т + п –1 = 8, т.е. необходимо иметь 8 загруженных клеток, что мы и имеем. Итак, по нашему варианту транспортные расходы составят:

150 • 2 + 10 • б + 170 • 5 + 70 • 2 + 100 • 6 + + 30 • 4+ 120 – 4 + 50 – 4 = 2750 тыс.руб.

Проверим исходный план на оптимальность. Для этого необходимо определить индексы U_i и V_j. Индексы определяются для загруженных клеток. Сумма индексов U_i и V_j должна быть равна транспортным издержкам C_ij, т.е. U₁+V₁=C₁₁; U₁+V₂ = C₁₂ В нашем примере значения Ui и Vj должны быть такими, чтобы U₁+V₁ = 2; U₁+V₂= 6; U₂+V₂ = 5; U₂+V₃ = 2; U₃+V₃ = 6; U₄+V₃ = 4; U₄+V₄ = 4; U₄ + V₅ = 4.

Индексы определяем следующим образом. Принимаем U1 = 0, так как U₁+V₁ = 2, то V₁=2–0 = 2.

Аналогично определяем значение V₂ = 6 – 0 = 6.

Далее определяем индекс U₂. Так как U₂ + V₂ = 5, а V₂ = 6, то U₂ + V₂ = 5, V₂ = 6, U₂ = 5 – 6 =1.

Определяем индекс V₃. Исходя из того, что U₂ + V₃ = 2, его значение равно: V₃ = 2 – (-1) = 3. Так определяет все значения U_i и V_j.

Далее исчисляем значения U_i + V_j и записываем в свободные квадраты.

Записанные значения сумм U_i + V_j в свободных квадратах 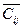, как правило, отличаются от значений C_ij (транспортные издержки).

При этом возможны три случая:

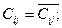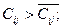1) 2) 3)

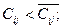
Сравниваем 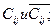определяем, является ли получен­ный вариант прикрепления потребителей к поставщикам опти­мальным. Если для всех свободных квадратов оказывается, что, 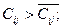то план считается оптимальным. Если хотя бы в одном из квадратов это условие не соблюдено, считается, что план не являет­ся оптимальным и его можно улучшить. В нашем примере (см. табл. 4) план не является оптимальным, так как 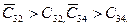Следовательно, его можно улучшить.

Улучшают вариант путем перемещения поставки в «свободные» квадраты, для которых 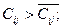. Если имеется несколько свободных квадратов, необходимо осуществлять перемещение для той, у кото­рой 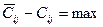. В нашем примере этот квадрат расположен в третьей строке второго столбца (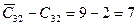). В другом квадрате эта разность меньше ().

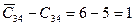В случае если разность окажется одинакова для сравниваемых свободных квадратов, следует выбирать один из них произвольно.

Итак, в рассматриваемом примере поставка должна быть пере­мещена в квадрат третьей строки и второго столбца. Перемещения производятся в определенном порядке с тем, чтобы не были наруше­ны условия, выраженные в приведенных выше уравнениях. Для этого образуем связку, т.е. замкнутую ломаную линию, состоящую из гори­зонтальных и вертикальных отрезков таким образом, чтобы одной из вершин образованного многоугольника был сам свободный квадрат, а остальные вершины находились бы в занятых квадратах.

Свободный квадрат может быть соединен четырьмя прямыми отрезками, с соседними занятыми квадратами, как это показано ниже.

После образования связи свободному квадрату и связанным с ним загруженным квадратам присваиваем поочередно знаки «—» или «+», начиная со свободного квадрата. В приведенном выше примере показана расстановка знаков. Направление расстановки знаков безразлично.

Далее просматриваем те занятые квадраты, которым присвоен знак «+», и выбираем тот из них, в котором содержится наимень­шая поставка; в рассматриваемом примере она равна 100 т. Именно это значение подлежит перемещению из каждого квадрата со знаком «+» в каждый квадрат (в том числе и свободный) со знаком «-». Пе­ремещение выглядит так:

II столбец III столбец

+ II строка	-
- свободный III строка	+

	Свободный

Рис. 10. Перемещение загрузки квадратов

В результате перемещения получаем новый вариант прикрепле­ния (табл. 5).

Таблица 5

Оптимальный план прикрепления потребителей к поставщикам

	Потребители	j = 1	j = 2	j = 3	j = 4	j = 5	Ресурсы поставщиков
Поставщики	Vj	V1=2	V2=6	V3=3	V4=3	V5=3
Ui
i = 1	U1=0
i = 2	U2= -1
i = 3	U3=4			-1	-1	-1
i = 4	U4=1
Потребности потребителей

Транспортные расходы предприятия составляют 2050 руб., т.е. они на 700 руб. меньше, чем в первом варианте.