Пусть а – фиксированное число, такое, что а > 0 и 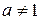 . Рассмотрим неравенства
. Рассмотрим неравенства
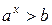 (1)
(1)
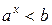 (2)
(2)
Область допустимых значений этих неравенств совпадает со всей числовой прямой, функция 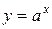 положительна и строго монотонна, следовательно, при
положительна и строго монотонна, следовательно, при 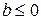 неравенство (1) выполняется при любом х из области допустимых значений, а неравенство (2) не имеет решений. При
неравенство (1) выполняется при любом х из области допустимых значений, а неравенство (2) не имеет решений. При 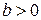 приходится рассмотреть два случая: а > 1 и 1 > a > 0.
приходится рассмотреть два случая: а > 1 и 1 > a > 0.
Пусть а > 1, тогда на всей числовой прямой функция 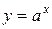 является возрастающей (рис.1). Значение, равное b, она принимает в единственной точке
является возрастающей (рис.1). Значение, равное b, она принимает в единственной точке 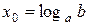 , и поэтому решением неравенства (1) является все
, и поэтому решением неравенства (1) является все 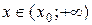 , а решением неравенства (2) – все
, а решением неравенства (2) – все 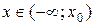 .
.
Пусть 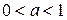 , тогда на всей числовой прямой функция
, тогда на всей числовой прямой функция 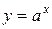 является убывающей (рис.2), и поэтому решением неравенства (1) являются все
является убывающей (рис.2), и поэтому решением неравенства (1) являются все 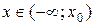 , а решением неравенства (2) – все
, а решением неравенства (2) – все 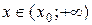 , где
, где 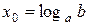 .
.
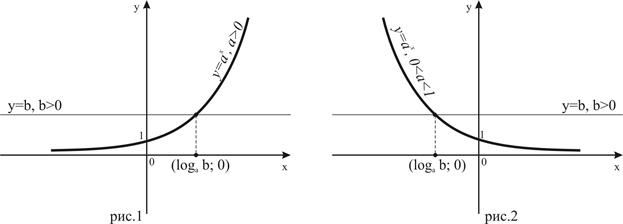
Изобразим изложенное выше в виде следующей наглядной схемы
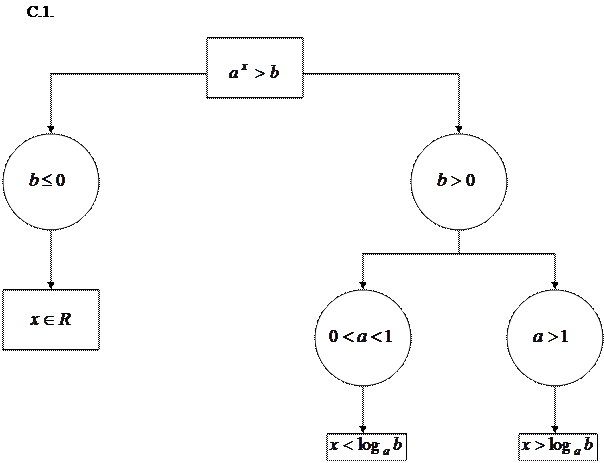 | |
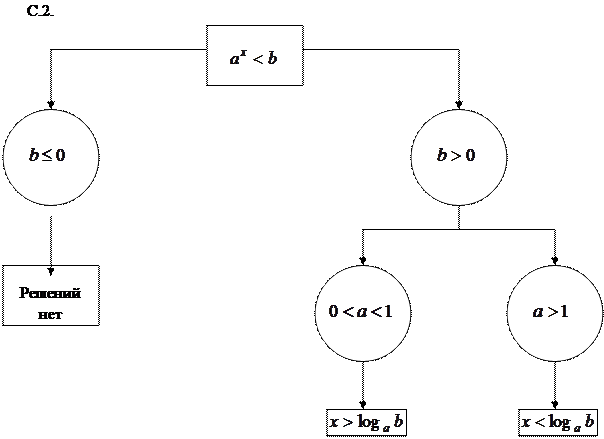 |
Пример 1.
Для каждого значения а решить неравенство
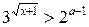 .
.
Решение.
Запишем неравенство в виде:
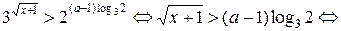
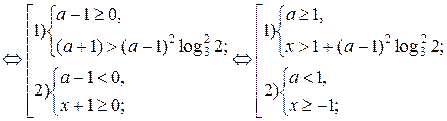
Ответ: при 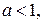
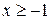 ; при
; при 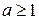 ,
, 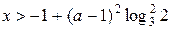
Таким образом, различные типы показательных неравенств сводятся к решению простейших показательных неравенств.
Рассмотрим неравенство вида:
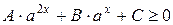 .
.
Решение.
Обозначив 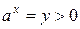 , получим
, получим 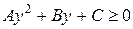 . Пусть решение последнего неравенства имеет вид:
. Пусть решение последнего неравенства имеет вид:
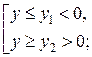
где 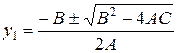 и
и 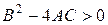 .
.
Тогда простейшее неравенство 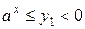 не имеет решений, а неравенство
не имеет решений, а неравенство 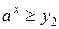 решается по схеме 1. Сразу выпишем в этом случае ответ.
решается по схеме 1. Сразу выпишем в этом случае ответ.
Ответ: при 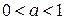 ,
, 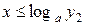 ;
;
при 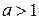 ,
, 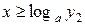
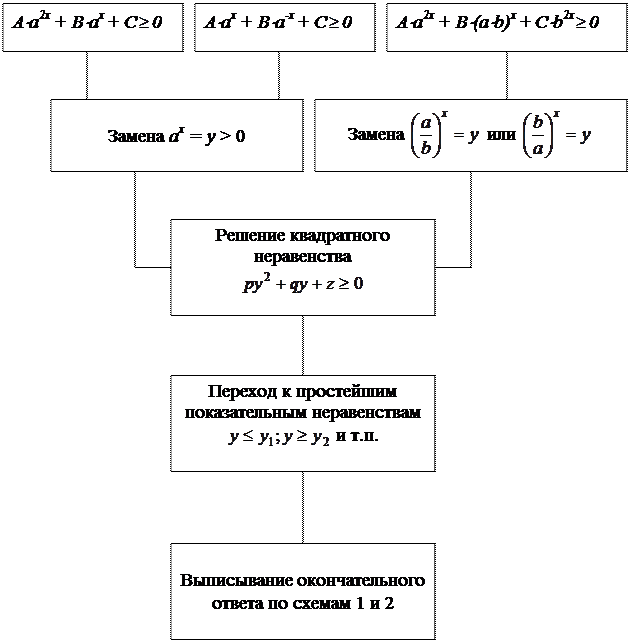 Сформулируем в виде краткой схемы решение трех аналогичных показательных неравенств.
Сформулируем в виде краткой схемы решение трех аналогичных показательных неравенств.
Заметим, что в предложенных выше схемах при решении неравенств многократно использовалось свойство положительности функции 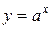 .
.
Пример.
Решить неравенство 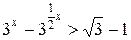 .
.
Решение.
Преобразуем неравенство 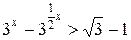 . В обозначениях
. В обозначениях 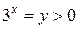 ,
, 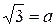 неравенство примет вид:
неравенство примет вид:
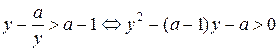 .
.
Найдем корни соответствующего уравнения 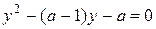
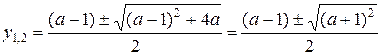 ,
,
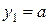 ,
, 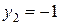 .
.
Причем 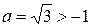
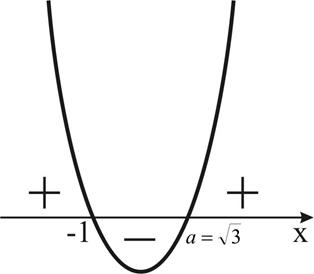
Значит неравенство равносильно совокупности
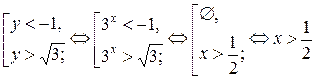
Ответ: 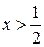 .
.
Рассмотрим следующий тип неравенств: 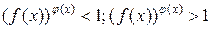 .
.
Решение.
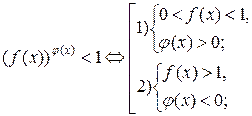
Аналогично решается и неравенство вида 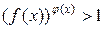 .
.
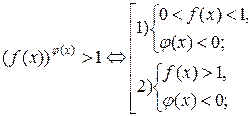
Пример.
Решить неравенство 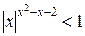
Решение.
По данной схеме неравенство равносильно совокупности двух систем:
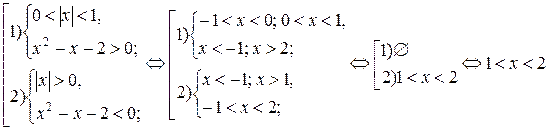
Ответ: 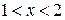
Кроме предложенных выше видов неравенств, предлагается решить графически неравенства, которые нельзя решить аналитически.
Пример.
а) 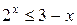
б) 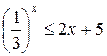
Решение.
а) 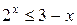
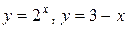
1. 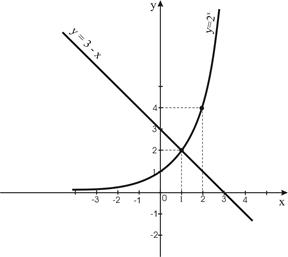 Построим графики функций
Построим графики функций 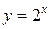 и
и 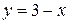 .
.
2. Найдем точки пересечения графиков функций 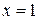 .
.
3. Решением данного неравенства будут те значения х, для каждого из которых график функции 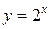 лежит ниже графика
лежит ниже графика 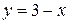 .
.
Ответ: 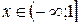
б) 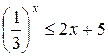
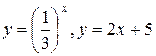
1. 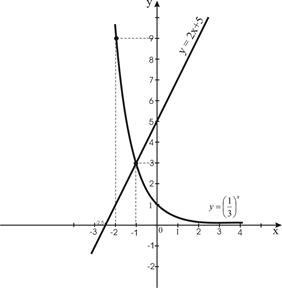 Построим график функций
Построим график функций 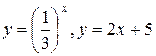 .
.
2. Найдем точки пересечения графиков функций.
3. Решением данного неравенства будут те значения х, для каждого из которых график функции 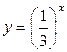 лежит ниже графика
лежит ниже графика 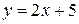 .
.
Ответ: 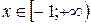 .
.
Приведем примеры решения аналогичного неравенства с дополнительным заданием.
Пример.
Найдите наибольшее целое решение неравенства.
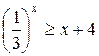 .
.
Анализ неравенства показывает, что в левой его чести записана показательная функция, а в правой – многочлен первой степени. Из этого следует, что решение можно проводить функционально-графическим методом.
Наличие только одной точки пересечения графиков функций 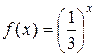 и
и 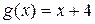 следует из того, что первая функция убывает, а вторая возрастает на
следует из того, что первая функция убывает, а вторая возрастает на 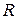 .
.
Решение.
Схематично изобразим графики функций 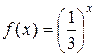 и
и 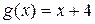 .
.
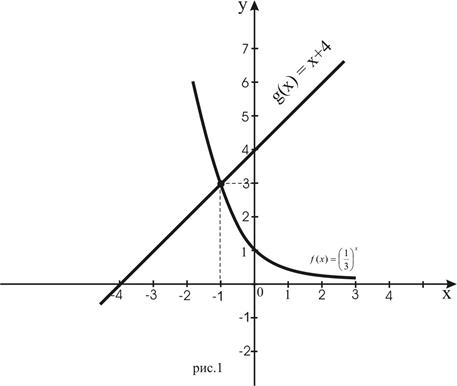
Из рисунка видно, что 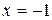 является корнем уравнения
является корнем уравнения 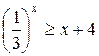 , так как
, так как 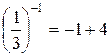 . График показательной функции расположен выше графика линейной функции при
. График показательной функции расположен выше графика линейной функции при 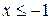 . Наибольшим целым решением неравенства является число –1.
. Наибольшим целым решением неравенства является число –1.
Ответ: –1.
Пример.
При каких значениях а значение выражения 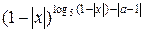 больше значения выражения
больше значения выражения 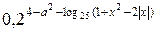 при всех допустимых значениях х?
при всех допустимых значениях х?
Решение.
1. Перейдем к одинаковому основанию степени в обоих выражениях:
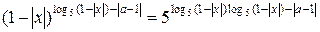
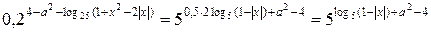
2. Введем новую переменную 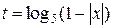 . Ее наибольшее значение равно нулю, а при стремлении х к 1 эта переменная стремится к
. Ее наибольшее значение равно нулю, а при стремлении х к 1 эта переменная стремится к 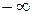 . В силу непрерывности функции получаем, что
. В силу непрерывности функции получаем, что 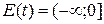 .
.
3. Относительно t получаем неравенство 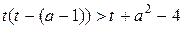 ,
, 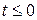 или
или 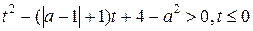 .
.
4. Абсцисса вершины параболы положительна, ветви направлены вверх. Значит, это неравенство верно при всех положительных t в том и только том случае, когда свободный коэффициент положителен. Следовательно, 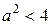
Ответ: (-2; 2).
В следующем примере решение показательного неравенства является составляющей более сложной задачи, а именно, нахождения области определения логарифмической функции.
Пример.
Найдите все значения параметра а, при которых в области определения функции 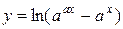 лежат числа 20, 50, 70, но не лежат числа 2, 5, 7.
лежат числа 20, 50, 70, но не лежат числа 2, 5, 7.
Решение.
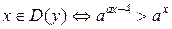 . При
. При 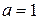 область определения пуста. Рассмотрим два случая.
область определения пуста. Рассмотрим два случая.
1) 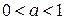 . Тогда
. Тогда 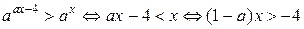 .
.
Так как 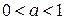 , то
, то 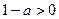 . Значит,
. Значит, 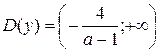 . Но в этом промежутке лежат все положительные числа и, в частности, числа 2, 5, 7. Поэтому такие значения
. Но в этом промежутке лежат все положительные числа и, в частности, числа 2, 5, 7. Поэтому такие значения 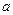 не удовлетворяют условию.
не удовлетворяют условию.
2) 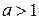 . Тогда
. Тогда 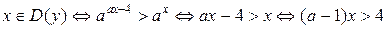 . Так как
. Так как 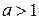 , то
, то 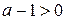 . Значит,
. Значит, 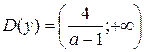 .
.
В этом промежутке лежат числа 20, 50, 70, только если его левый конец меньше 20. А для того, чтобы в нем не было чисел 2, 5, 7, нужно, чтобы левый конец был не меньше 7. Получается двойное неравенство на параметр 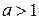 .
.
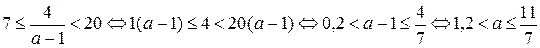 .
.
Ответ: 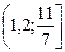 .
.
Рассмотрим следующий пример. В нем исследуется композиция (результат последовательного выполнения) трех базовых функций: показательной с основанием 3, затем с обратно пропорциональной зависимостью и, наконец, показательной с основанием 2.
Пример.
Найдите множество значений функции
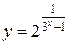
Решение.
Функция определена при 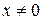 . Рассмотрим случай
. Рассмотрим случай 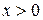 . По свойствам показательной функции с основанием 3, при неограниченном возрастании х величина
. По свойствам показательной функции с основанием 3, при неограниченном возрастании х величина 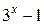 также неограниченно возрастает от нуля к
также неограниченно возрастает от нуля к 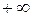 . Так как числитель дроби
. Так как числитель дроби 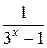 постоянен, а знаменатель неограниченно возрастает, оставаясь положительными, то сама дробь убывает от
постоянен, а знаменатель неограниченно возрастает, оставаясь положительными, то сама дробь убывает от 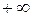 к нулю, оставаясь положительной. Так как показательная функция с основанием 2 сохраняет характер монотонности, то получаем, что при таком изменении аргумента х функция у убывает от
к нулю, оставаясь положительной. Так как показательная функция с основанием 2 сохраняет характер монотонности, то получаем, что при таком изменении аргумента х функция у убывает от 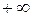 до
до 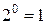 . Значит, при положительных х данная функция принимает все значения от 1 до
. Значит, при положительных х данная функция принимает все значения от 1 до 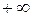 .
.
Аналогичным образом при убывании отрицательного аргумента х от нуля к 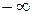 величина
величина 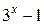 убывает от нуля к –1, а значит, величина
убывает от нуля к –1, а значит, величина 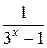 возрастает от
возрастает от 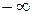 к –1, оставаясь меньше –1. Так как показательная функция с основанием 2 сохраняет характер монотонности, то при таком изменении аргумента х функция у монотонно и непрерывно возрастает от 0 к
к –1, оставаясь меньше –1. Так как показательная функция с основанием 2 сохраняет характер монотонности, то при таком изменении аргумента х функция у монотонно и непрерывно возрастает от 0 к 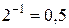 . Значит, при отрицательных х данная функция принимает все значения от 0 до 0,5. Остается объединить ответы.
. Значит, при отрицательных х данная функция принимает все значения от 0 до 0,5. Остается объединить ответы.
Ответ: 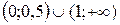 .
.
Приведенное решение максимально точно соответствует характеру задания функции. Уж раз сама исследуемая функция есть результат последовательного выполнения трех различных элементарных композиций, то и множество ее значений следует искать последовательно на каждом поле выполняя необходимые вычисления.
В основу решения некоторых неравенств удается положить следующее простое наблюдение: если известно что, например, функция 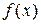 монотонно возрастает на своей области определения Е и
монотонно возрастает на своей области определения Е и 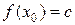 , то множеством решений неравенства
, то множеством решений неравенства 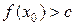 является множество
является множество  . Докажем это утверждение.
. Докажем это утверждение.
Если 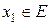 и
и 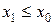 , то
, то 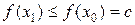 , то есть в точке
, то есть в точке 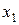 неравенство
неравенство 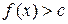 не выполняется. Если же
не выполняется. Если же 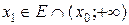 , то
, то 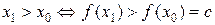 . То есть неравенство выполняется на множестве
. То есть неравенство выполняется на множестве 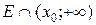 и только на нем. Что и требовалось доказать.
и только на нем. Что и требовалось доказать.
В случае неравенств с показательной функцией рассмотренное утверждение применяется, например, в следующей ситуации:
Решить неравенство
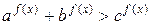 ,
,
выполняется одна из двух систем условий:
1) 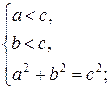 или 2)
или 2) 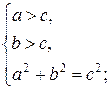
Решение
Приведем неравенство к виду:
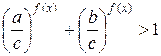
Заменив 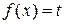 , рассмотрим функцию
, рассмотрим функцию
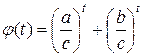 . Тогда
. Тогда 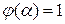 .
.
Кроме того, оба основания
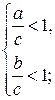 или
или 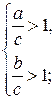 ,
,
поэтому функция 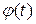 монотонно убывает в первом случае и монотонно возрастает в случае (2), как сумма двух функций монотонно убывает или монотонно возрастает для
монотонно убывает в первом случае и монотонно возрастает в случае (2), как сумма двух функций монотонно убывает или монотонно возрастает для 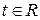 .
.
Согласно доказанному выше утверждению, искомое неравенство сводится теперь к одному из неравенств 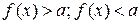 .
.
Пример.
Числа а и b являются длинами катетов, а число с – длина гипотенузы прямоугольного треугольника. Определить знак числа 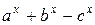 для всех значений переменной х.
для всех значений переменной х.
Решение.
Задача сводится к решению неравенства  . По теореме Пифагора, выполняется система условий:
. По теореме Пифагора, выполняется система условий:
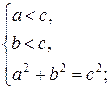
Значит, функция 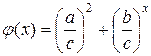 убывает, и
убывает, и 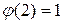 . Тогда
. Тогда 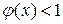 при
при 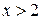 и
и 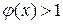 при
при 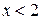 , чему соответствует следующий
, чему соответствует следующий
Ответ: 
Таким образом, в этом параграфе рассматривались различные примеры решений показательных неравенств с использованием свойств показательной функции.
 2015-07-03
2015-07-03 3347
3347








