Определение условного экстремума функции многих переменных

Для случая, когда число переменных n не меньше двух (n≥2) вводится понятие условного экстремума. Экстремум функции многих переменных, достигаемый по какой-то отдельной переменной x_j, называется условным экстремумом данной функции. Достигается этот условный экстремум в точке 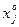, в которой 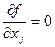. Точка Х⁰=(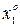, , 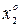, 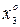…), в которой все частные производные функции Z=f(X) равны 0, называется стационарной точкой.

Необходимое условие экстремума. Если в точке Х* функция Z=f(X) имеет экстремум, то все частные производные функции в этой точке равны нулю:

f′_xi(X*) = 0, i=1,2, …, n.

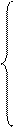Следовательно, точки экстремума функции Z=f(X) удовлетворяют системе уравнений:

f′_x1 (х₁, х₂, …, х_n)= 0,

f′_x2 (х₁, х₂, …, х_n)= 0,

...... (7.5)

f′_xn (х₁, х₂, …, х_n)= 0,

Таким образом, любая точка экстремума ФМП есть точка стационарная, то есть, Х^*=Х⁰. Обратное верно не всегда.

Как и в случае одной переменной, необходимое условие не является достаточным для того, чтобы стационарная точка была точкой экстремума: это может быть точкой изгиба функции. Для получения условий достаточности экстремума ФМП следует определить в стационарной точке знак дифференциала второго порядка. Если от частной производной 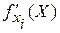найти частную производную по переменной x_j, то получим частную производную второго порядка по переменным x_i, x_j, которая обозначается 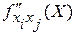. Дифференциал второго порядка обозначается d²f(х₁, х₂, …, х_n)=d²f(X) и равен сумме произведений частных производных второго порядка по всем переменным (аргументам) на соответствующие приращения этих переменных, то есть

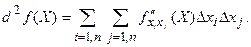(7.6)

Достаточные условия экстремума:

а) в стационарной точке Х^о функция Z=f(X) имеет максимум, если d²f(X⁰)<0, и минимум, если d²f(X^о)>0, при любых Δх_i и Δх_j, не обращающихся в нуль одновременно (в этих случаях Х^о = Х*);

б) если d²f(X^о) может принимать в зависимости от Δх_i и Δх_j и положительные, и отрицательные значения, то в точке Х^о функция Z=f(X) экстремума не имеет (может иметь место изгиб функции);

в) если d²f(X^о) может обращаться в нуль не только при нулевых приращениях Δх_i и Δх_j, то вопрос об экстремуме остается открытым.

Для функции двух переменных Z=f(x₁,x₂) достаточные условия еще не очень сложны. Существуют четыре частные производные второго порядка: 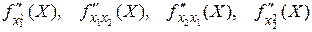. Из них две смешанные производные 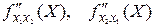, если непрерывны, то равны.

Найдем значения частных производных второго порядка в стационарной точке 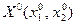и обозначим:

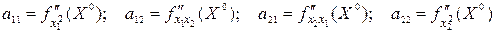
(можно убедиться, что а₁₂=а₂₁).

Обозначим через Δ определитель, составленный из a_ij для i, j = 1, 2:

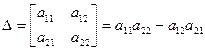(7.7)

Тогда достаточные условия экстремума для функции двух переменных примут вид:

а) если Δ>0 и а₁₁<0 (a₂₂<0), то в точке Х⁰ функция имеет максимум; если Δ>0 и а₁₁>0 (a₂₂>0), то в точке Х⁰ – минимум (в этих случаях Х⁰= Х^*);

б) если Δ>0, то функция в этой точке экстремума не имеет;

в) если Δ=0, то вопрос об экстремуме остается открытым.

Схема определения экстремума функции n переменных совпадает с правилами определения локального экстремума функции одной переменной.

...........

Как правило, в практических задачах необходимо определить наибольшее и наименьшее значения функции (глобальный экстремум) в некоторой области.

Говорят, что функция Z=f(X) в точке Х⁰ заданной области D имеет глобальный максимум (наибольшее значение) или глобальный минимум (наименьшее значение), если неравенство f(X)≤ f(X⁰) или f(X)≥ f(X⁰), соответственно, выполняется для любой точки XЄD.

Теорема Вейерштрасса (Weierstras, Карл Теодор Вильгельм-нем. математик, 1815-1897). Если область D замкнута и ограничена, то дифференцируемая функция Z=f(X) достигает в этой области своих наибольшего и наименьшего значений или в стационарной точке, или в граничной точке области.

Следовательно, чтобы найти наибольшее (наименьшее) значения функции Z=f(X) в области D, нужно:

1) найти все стационарные точки внутри области D и вычислить значения функции в них;

2) исследовать функцию на экстремум на границе области D и вычислить значения функции на границах области D;

3) сравнить значения функции, полученные в п.1 и 2: наибольшее (наименьшее) из этих чисел и будет наибольшим (наименьшим) значением функции во всей области.

Граница области D аналитически может быть задана системой уравнений (условий) относительно переменных х₁, х₂, …, x_n. Поэтому, исследуя экстремальные свойства функции на границах области D, необходимо решить задачу определения условного экстремума.