Основные теоретические положения

Рассмотрим схему колебательного контура, приведенную на рис. 7.1, которая запитана от источника постоянного тока 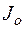. Нелинейный элемен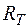т имеет 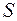-образную ВАХ, показанную на рис. 7.2.

Для упрощения аппроксимируем данную нелинейную характеристи­ку тремя отрезками прямых лини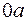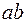й , и 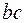. Произведем анализ цепи для каждого из участков ВАХ нелинейного элемента .

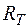1. На участке 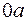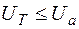, , 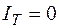следовательно, 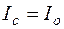(допускаем протекание постоянного тока через конденсатор за счет наличия в нем утечек). На рис. 7.3 приведена схема замещения цепи для участка .

,

.

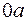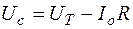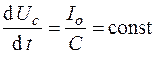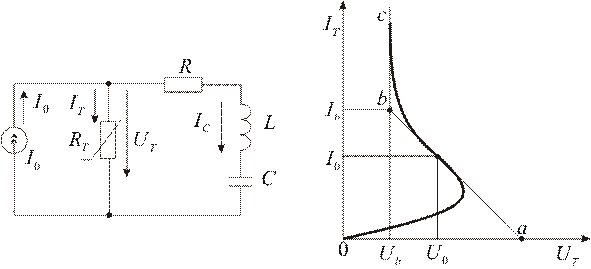
Рис. 7.1 Рис. 7.2

2. На участке 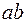нелинейный элемент характеризуется отри­цательным дифференциальным сопротивлением

.

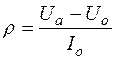Схема замещения для этого случая приведена на рис. 7.4. Нелинейный элемент заменяется источником ЭДС 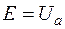и сопротивлением .

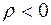Дифференциальное уравнение контура представляется в виде

.

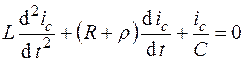Корни характеристического уравнения

.

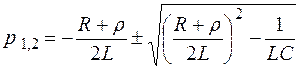В зависимости от соотношения между 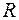и 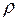вещественная часть корней может быть либо положительной (расходящийся переходный процесс), либо отрицательной (затухающий переходный процесс).

3. Схема замещения участка 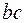показана на рис. 7.5. Дифференциальное уравнение контура

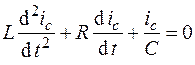
имеет корни характеристического уравнения

.

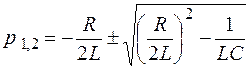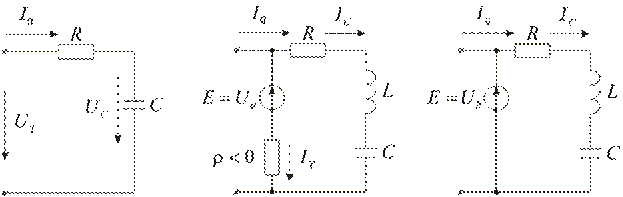
Рис. 7.3 Рис. 7.4 Рис. 7.5

Переходные процессы, происходящие в нелинейном колебательном контуре на каждой из аппроксимирующих линий ВАХ, наглядно представляются на фазовой плоскости. По оси 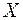фазовых плоскостей, показанных на рис. 7.6 и 7.7, отложено напряжение на конденсаторе, а по оси 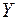– его производная .

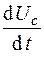Если для участков 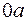и 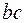ВАХ нелинейного элемента характерны лишь затухающие переходные процессы, отображенные на рис. 7.6, то для участка 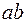возможны и расходящиеся переходные процессы, показанные на рис. 7.7.

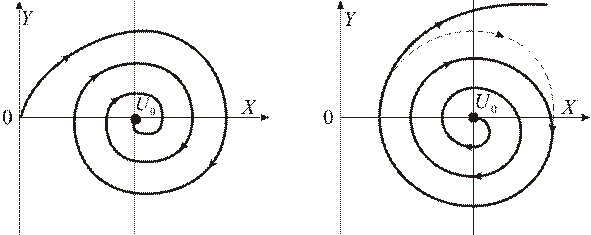
Рис. 7.6 Рис. 7.7

Режим незатухающих колебаний характеризуется замкнутой кривой, называемой предельным циклом (показан пунктиром на рис. 7.7).