Простые числа. Проверка чисел на простоту. Тест Рабина- Миллера

Простое число — это натуральное (целое положительное) число, имеющее ровно два различных натуральных делителя. Другими словами, число p простое, если оно больше 1 и делится без остатка только на 1 и на p.

Тестом простоты называется алгоритм, который, приняв на входе число 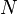, позволяет либо не подтвердить предположение о составности числа, либо точно утверждать его простоту. Во втором случае он называется истинным тестом простоты. Таким образом, тест простоты представляет собой только гипотезу о том, что если алгоритм не подтвердил предположение о составности числа 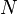, то это число может являться простым с определенной вероятностью.

Тест Миллера — Рабина — вероятностный полиномиальный (очень быстрый) тест простоты.

Для теста Миллера — Рабина используется следующее утверждение:

Пусть 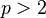— простое число. Представим число 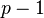в ви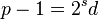де , где 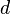— нечётно. Тогда для любого a из Zp выполняется одно из условий:

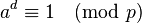
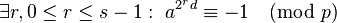
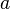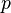Если это утверждение выполняется для некоторых чисел и , то число 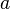называют свидетелем простоты числа 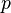, а само число 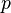— вероятно простым.

В случае, если найдется число 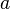такое, что:

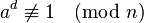
и

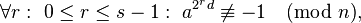
то число 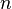не является простым. В этом случае число 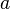называют свидетелем того, что число 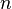составное.