Задача 2

Для трехпараметрической модели найти ожидаемое время выполнения проекта, определить вероятность выполнения проекта не позднее заданного срока, найти интервал гарантированного (Р = 0,9973) времени выполнения проекта, оценить максимально возможный срок выполнения проекта с заданной надежностью.

Работа	Опирается на работы	t пес.	t вер.	t опт.
b 1 b 2 b 3 b 4 b 5 b 6 b 7 b 8 b 9 b 10 b 11	- - - b 1 b 1 b 3 b 2, b 5, b 6 b 2, b 5, b 6 b 4, b 7 b 3 b 2, b 5, b 6, b 10

Директивный (заданный) срок выполнения проекта T _дир. = 21 день.

Заданная надежность γ = 0,95.

Выполнить те же расчеты для двухпараметрической модели. Сравнить результаты.

Решение.

Найдем ожидаемую продолжительность работ (t _ож.) для трехпараметрической модели по формуле

t _ож. = .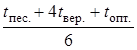

Например, t _ож.(b ₁) = ;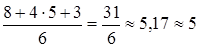

t _ож.(b ₂) = ;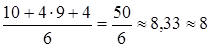

t _ож.(b ₃) = ;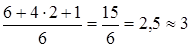

t _ож.(b ₄) = ;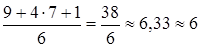

t _ож.(b ₅) = ;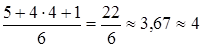

и т.д.

Для упрощения дальнейших вычислений округляем полученные величины до целых чисел (по правилам округления с избытком и недостатком).

Для сравнения найдем также ожидаемую продолжительность работ (t* _ож.) для двухпараметрической модели по формуле

t* _ож. = .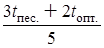

Например, t* _ож.(b ₁) = ;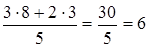

t* _ож.(b ₂) = ;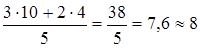

t* _ож.(b ₃) = ;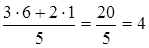

t* _ож.(b ₄) = ;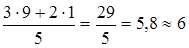

t* _ож.(b ₅) = ;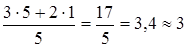

и т.д.

Двухпараметрическая модель проще, но дает менее точные оценки.

Для вычисления дисперсий продолжительностей работ воспользуемся формулой σ²(t _ож.) =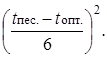

σ²(t _ож.(b ₁)) =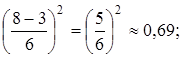

σ²(t _ож.(b ₂)) =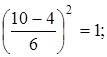

σ²(t _ож.(b ₃)) =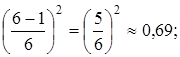

σ²(t _ож.(b ₄)) =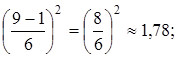

σ²(t _ож.(b ₅)) =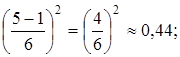

и т.д.

Дополним исходную таблицу полученными значениями:

Работа	Опирается на работы	t пес.	t вер.	t опт.	t ож.	t* ож.	σ2
b 1 b 2 b 3 b 4 b 5 b 6 b 7 b 8 b 9 b 10 b 11	- - - b 1 b 1 b 3 b 2, b 5, b 6 b 2, b 5, b 6 b 4, b 7 b 3 b 2, b 5, b 6, b 10						0,69 1,00 0,69 1,78 0,44 0,03 0,25 2,25 1,36 3,36 1,78

Таким образом трехпараметрическая модель сведена к однопараметрической.

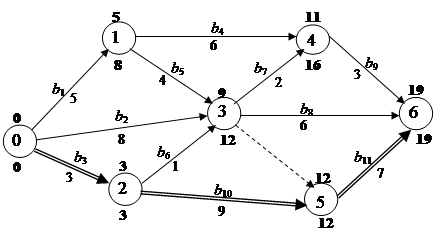Теперь можно построить сетевой график и рассчитать его временные характеристики.

Рис. 4

Работа	Опирается на работы	t ож.	σ2
b 1 b 2 * b 3 b 4 b 5 b 6 b 7 b 8 b 9 * b 10 * b 11	- - - b 1 b 1 b 3 b 2, b 5, b 6 b 2, b 5, b 6 b 4, b 7 b 3 b 2, b 5, b 6, b 10		0,69 1,00 0,69 1,78 0,44 0,03 0,25 2,25 1,36 3,36 1,78

Ожидаемое критическое время Т _кр = 19.

На критическом пути лежат работы b ₃, b ₁₀, b ₁₁.

Найдем дисперсию критического пути.

σ²_кр = σ²(b ₃) + σ²(b ₁₀) + σ²(b ₁₁) = 0,69 + 3,36 + 1,78 = 5,83.

Среднеквадратическое отклонение критического пути σ_кр =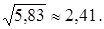

Найдем вероятность того, что проект будет выполнен не позднее заданного срока (Т _дир = 21 день):

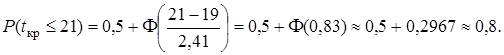
Таким образом, имеются неплохие шансы (80 %) выполнить проект в заданный срок.

Найдем интервал гарантированного времени выполнения проекта. Воспользуемся правилом «трех сигм»: 3σ_кр =3 2,41 = 7,23 , т.е. с вероятностью почти 0,9973 проект будет выполнен за 19 7 дней.

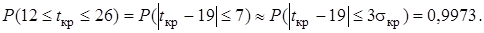
(Более точное значение:

)

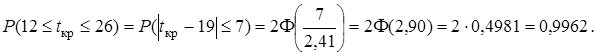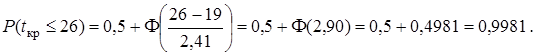
Следовательно, можно с большой долей уверенности гарантировать, что максимальный срок выполнения проекта не превысит 26 дней.

Оценим максимально возможный срок T выполнения проекта с заданной надежностью γ = 0,95.

По таблице значений функции Лапласа найдем доверительный коэффициент z _γ для заданной надежности γ.

Так как 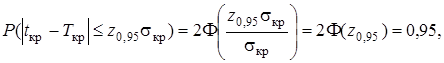то из

2Φ(z _0,95) = 0,95, 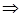Φ(z _0,95) = 0,475, 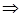z _0,95 = 1,96 и

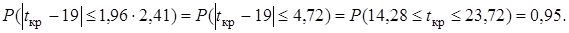
Это значит, что с надежностью 0,95 проект будет завершен в период от 14 до 24 дней.

Более точную оценку максимально возможного срока Т завершения проекта с данной надежностью γ можно получить из формулы

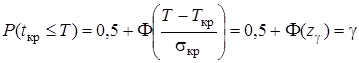, где Т – Т _кр = z _γσ_кр.

В нашем случае 0,5 + Φ(z _0,95) = 0,95, 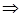Φ(z _0,95) = 0,45, z _0,95 = 1,65 и

Т = Т _кр + z _γσ_кр = 19 + 1,65 2,41 19 + 3,98 = 22,98 23, т.е. с надежностью 0,95 проект будет завершен не позже 23 дней.

Здесь использована функция Лапласа вида Φ(x) = .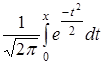

Следует также помнить, что функция Лапласа данного вида нечетная, т.е. Φ(– x) = – Φ(x), а при x ≥ 5 значение Φ(x) ≈ 0,5.

Для двухпараметрической модели будем иметь:

Работа	Опирается на работы	t пес.	t опт.	t* ож.	σ2
b 1 b 2 b 3 b 4 b 5 b 6 b 7 b 8 b 9 b 10 b 11	- - - b 1 b 1 b 3 b 2, b 5, b 6 b 2, b 5, b 6 b 4, b 7 b 3 b 2, b 5, b 6, b 10				0,69 1,00 0,69 1,78 0,44 0,03 0,25 2,25 1,36 3,36 1,78

Проведем анализ полученной однопараметрической модели. Найдем временные характеристики событий и работ. Построим структурный сетевой график.

Рис. 5

Сроки наступления и резервы времени событий:

Событие	Ранний срок T p(i)	Поздний срок T п(i)	Резерв времени R (i)
* 0 * 2 * 5 * 6

Критический путь проходит через события с нулевым резервом времени, т.е. через события 0, 2, 5, 6. Критическое время Т _кр = 24 дня.

Характеристики работ:

Работа	t* ож.	σ2	S p(bi)	S п(bi)	E p(bi)	E п(bi)	r п(bi)	r c(bi)
b 1 = (0,1) b 2 = (0,3) * b 3 = (0,2) b 4 = (1,4) b 5 = (1,3) b 6 = (2,3) b 7 = (3,4) b 8 = (3,6) b 9 = (4,6) *b 10 = (2,5) *b 11 = (5,6) φ = (3,5)		0,69 1,00 0,69 1,78 0,44 0,03 0,25 2,25 1,36 3,36 1,78						-6 -6 -6

φ = (3,5) – фиктивная работа.

Критические работы – b ₃, b ₁₀, b ₁₁. Резервы времени этих работ равны нулю.

Найдены наиболее ранние и наиболее поздние сроки начала и окончания каждой работы.

Наиболее ранний возможный срок начала работы b_i = (k, j):

S _p(b_i) = S _p(k, j) = T _p(k);

Наиболее поздний допустимый срок начала работы b_i = (k, j):

S _п(b_i) = S _п(k, j) = T _п(j) – t_kj;

Наиболее ранний возможный срок окончания работы b_i = (k, j):

E _p(b_i) = E _p(k, j) = T _p(k) + t_kj;

Наиболее поздний допустимый срок окончания работы b_i = (k, j):

E _п(b_i) = E _п(k, j) = T _п(j);

Полный резерв работы b_i = (k, j) можно найти и проверить по формулам:

r _п(b_i) = r _п(k, j) = T _п(j) – T _p(k) – t_kj = S _п(b_i) – S _p(b_i) = E _п(b_i) – E _p(b_i).

Свободный резерв работы b_i = (k, j) может быть найден по формуле

r _с(b_i) = r _с(k, j) = T _р(j) – T _п(k) – t_kj.

Резервы времени и коэффициенты напряженности некритических дуг:

Некритические дуги	Резерв времени дуги, R (b)	Коэффициент напряженности дуги, N (b)
(2,3,5) (0,3,5) (0,1,3,5) (0,3,6) (0,1,3,6) (0,1,4,6) (0,1,3,4,6) (2,3,6) (2,3,4,6)		2/13 ≈ 0,15 8/17 ≈ 0,47 9/17 = 0,53 17/24 ≈ 0,71 18/24 ≈ 0,75 17/24 ≈ 0,71 17/24 ≈ 0,71 11/20 = 0,55 10/20 = 0,50

Итак, ожидаемое критическое время Т _кр = 24.

На критическом пути лежат работы b ₃, b ₁₀, b ₁₁.

Найдем дисперсию критического пути.

σ²_кр = σ²(b ₃) + σ²(b ₁₀) + σ²(b ₁₁) = 0,69 + 3,36 + 1,78 = 5,83.

Среднеквадратическое отклонение критического пути σ_кр =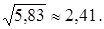

Найдем вероятность того, что проект будет выполнен не позднее заданного срока (Т _дир = 21 день):

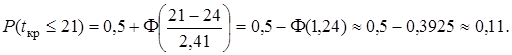
Вероятность выполнить проект в заданный срок очень невелика (11 %).

Найдем интервал гарантированного времени выполнения проекта. Воспользуемся правилом «трех сигм»: 3σ_кр =3 2,41 = 7,23 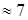, т.е. с вероятностью почти 0,9973 проект будет выполнен за 24 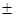7 дней.

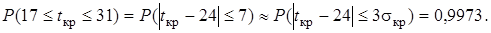
(Более точное значение:

)

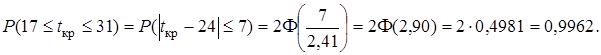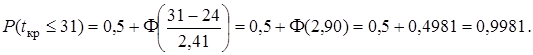
Следовательно, можно с большой долей уверенности гарантировать, что максимальный срок выполнения проекта не превысит 31 дня.

Оценим максимально возможный срок T выполнения проекта с заданной надежностью γ = 0,95.

По таблице значений функции Лапласа найдем доверительный коэффициент z _γ для заданной надежности γ.

Так как 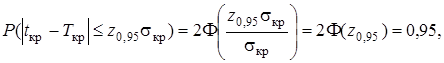то из

2Φ(z _0,95) = 0,95, 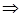Φ(z _0,95) = 0,475, 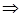z _0,95 = 1,96 и

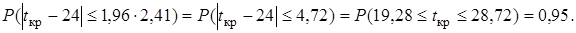
Это значит, что с надежностью 0,95 проект будет завершен в период от 19 до 29 дней.

Более точную оценку максимально возможного срока Т завершения проекта с данной надежностью γ можно получить из формулы

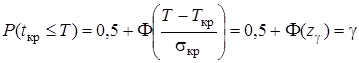, где Т – Т _кр = z _γσ_кр.

В нашем случае 0,5 + Φ(z _0,95) = 0,95, 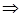Φ(z _0,95) = 0,45, 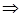z _0,95 = 1,65 и

Т = Т _кр + z _γσ_кр = 24 + 1,65 2,41 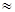24 + 3,98 = 27,98 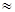28, т.е. с надежностью 0,95 проект будет завершен не позже 28 дней.

Рассмотрим самую напряженную некритическую дугу. Это дуга (0,1,3,6). Ее коэффициент напряженности 0,75. В зависимости от величины коэффициента напряженности выделяют три зоны: критическую (с коэффициентом напряженности большим 0,8), подкритическую (0,6 ≤ N (b) ≤ 0,8), резервную (N (b) < 0,6). Дуга (0,1,3,6) попадает в подкритическую зону. Найдем ее среднеквадратическое отклонение.

σ²(0,1,3,6) = σ²(0,1) + σ²(1,3) + σ²(3,6) = σ²(b₁) + σ²(b₅) + σ²(b₈) =

= 0,69 + 0,44 + 2,25 = 3,38.

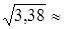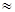σ (0,1,3,6) = 1,84 2.

Среднеквадратическое отклонение данной дуги (1,84) меньше среднеквадратического отклонения критического пути (2,41). Значит, ожидаемое значение этой дуги 18±1,84; это меньше, чем ожидаемое значение критической дуги (24±2,41), на которую эта некритическая дуга опирается. Это означает, что переход на эту дугу критического пути маловероятен. Поэтому рассматривать ее как претендента на критический путь не следует.

Если среднеквадратическое отклонение некритической дуги больше среднеквадратического отклонения критической дуги, на которую она опирается, и ожидаемое значение такой дуги с учетом этого отклонения может превысить ожидаемое значение опорной критической дуги, то следует найти вероятностные характеристики критического пути, проходящего через такую дугу. В качестве окончательного показателя выбирают наихудшие показатели альтернативных критических путей.

Если в сетевом графике имеются параллельные критические пути, то для расчета вероятностных характеристик нужно выбрать критический путь с наибольшим среднеквадратическим отклонением.