Теоретическая часть

Лабораторная работа №4

Исследование резонанса напряжений в простых электрических цепях

Цель работы: исследование резонанса напряжений и амплитудно-частотных характеристик последовательного колебательного контура.

В результате выполнения лабораторной работы студенты должны знать:

- условия возникновения резонанса;

- основные характеристики, относящиеся к явлению резонанса, определение характеристического сопротивления, добротности контура, затухания, полосы пропускания контура;

- влияние добротности контура на частотные характеристики;

Уметь:

- определять резонансную частоту контура, характеристическое сопротивление контура, добротность, затухание и полосу пропускания контура;

- производить настройку контура в резонанс;

- определять экспериментально их характеристики.

Задача работы – исследование и построение частотных характеристик параллельного колебательного контура.

Теоретическая часть

Рассмотрим изменение тока и напряжений на элементах цепи при синусоидальном входном воздействии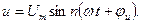

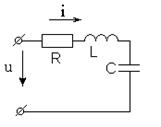
Согласно, второго закона Кирхгофа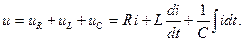

Запишем это уравнение в комплексной форме: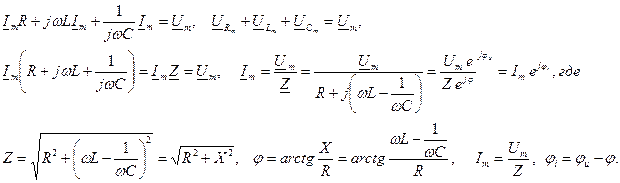

Мгновенное значение тока: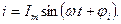

Напряжение на элементах:

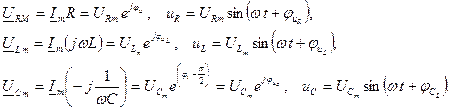
Токи и напряжения на различных участках электрической цепи синусоидального тока по фазе не совпадают. Наглядное представление о фазовом расположении различных векторов дает векторная диаграмма. На векторной диаграмме закон Кирхгофа выполняется в векторной форме:

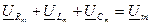
В зависимости от соотношения величин 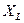и 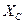возможны три различных случая:

1. 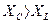, следовательно 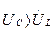. Этому режиму соответствует векторная диаграмма, изображенная на рис.1а.

2. 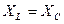, следовательно 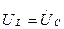- резонанс напряжений (рис. 1б).

3. 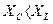, следовательно 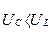. Этот случай изображен на рис.1с.

При условии резонанса напряжений 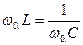из (1) и (2) следует,

что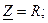

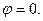
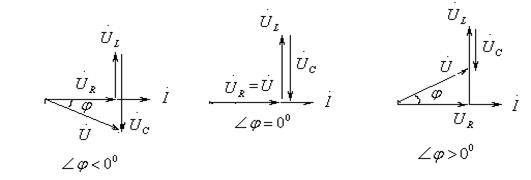
а) б) с)

Рисунок 1.

При резонансной частоте :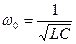

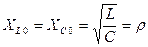
Это сопротивление называется характеристическим или волновым сопротивлением цепи.

При резонансе напряжения, входное сопротивление становится чисто резистивным, реактивное входное сопротивление равно нулю ,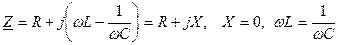

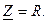
Резонансная частота контура определяется из соотношения 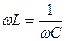, т.е. ,

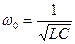Так как 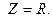Ток в цепи и мощность максимальны.

Напряжения на реактивных элементах равны по величине и противоположны по направлению. Реактивные мощности тоже равны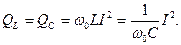

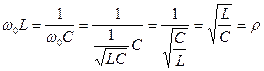- характеристическое или волновое сопротивление контура.

Отношение напряжений на реактивных элементах к приложенному напряжению, или отношение реактивных мощностей к активной мощности в режиме резонанса называется добротностью контура

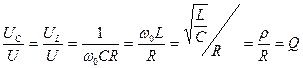- добротность контура.

Добротность контура указывает во сколько раз напряжение на индуктивности и емкости при резонансе больше, чем напряжение приложенное к цепи.

В области до резонанса при w<w₀ цепь носит ёмкостный характер, в резонансе (w=w₀) - активный, а после резонанса при w>w₀ – индуктивный характер.

Интервал частот на границах которого ток 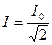называют полосой пропускания - 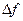. Относительная полоса пропускания называется затуханием цепи: .

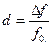Затухание цепи связано с добротностью контура соотношением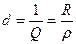

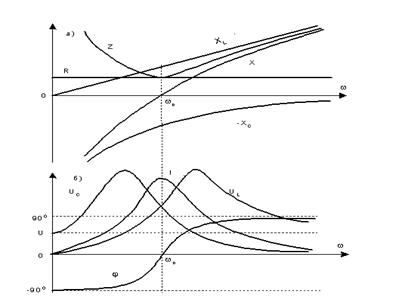
Рисунок 2