Граф автомата с 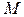 состояниями состоит из
состояниями состоит из 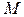 вершин, изображаемых кружками, причем каждая вершина соответствует состоянию автомата и обозначается символом этого состояния. Вершины графа могут соединяться друг с другом ребрами, изображаемыми в виде линий со стрелками, указывающими направление перехода из одного состояния в другое, которые проводятся и обозначаются по правилу: если
вершин, изображаемых кружками, причем каждая вершина соответствует состоянию автомата и обозначается символом этого состояния. Вершины графа могут соединяться друг с другом ребрами, изображаемыми в виде линий со стрелками, указывающими направление перехода из одного состояния в другое, которые проводятся и обозначаются по правилу: если 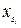 - символ, при воздействии которого автомат, находящийся в состоянии
- символ, при воздействии которого автомат, находящийся в состоянии 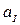 переходит в состояние
переходит в состояние 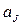 и при этом выдает некоторый символ
и при этом выдает некоторый символ 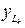 , то образуем пару (
, то образуем пару (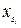 ,
, 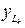 ).
).
Пусть 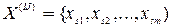 - множество всех входных символов, таких, что
- множество всех входных символов, таких, что 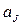 =
= 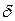 (
(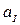 ,
, 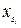 ),
), 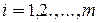 , и ему соответствует множество пар (
, и ему соответствует множество пар (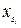 ,
, 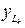 ),
), 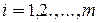 .
.
Тогда, если множество 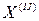 не пусто, то вершины
не пусто, то вершины 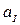 и
и 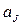 и построенное ребро отмечается дизъюнкцией пар
и построенное ребро отмечается дизъюнкцией пар 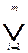 (
(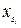 ,
, 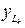 ). В случае, если
). В случае, если 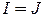 ребро начинается и заканчивается в одной и той же вершине
ребро начинается и заканчивается в одной и той же вершине 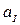 (рис.8).
(рис.8).
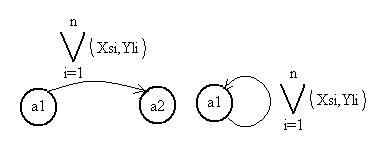
Рис.8
В случае автоматов Мура все ребра, входящие в одну и ту же вершину 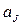 , должны отмечаться парами (
, должны отмечаться парами (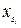 ,
, 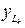 ), где
), где 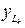 =
= 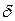 (
(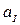 ), т.е. во всех парах пишется один и тот же выходной символ, отмечающий состояние
), т.е. во всех парах пишется один и тот же выходной символ, отмечающий состояние 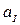 . Поэтому при изображении графа автомата Мура ребра отмечают только дизъюнкцией входных символов, а вершины графа дополнительно отмечают выходными символами, соответствующими данному состоянию.
. Поэтому при изображении графа автомата Мура ребра отмечают только дизъюнкцией входных символов, а вершины графа дополнительно отмечают выходными символами, соответствующими данному состоянию.
|
|
|
Из условия однозначности функций 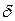 и
и 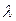 следует свойство графов, задающих конечные автоматы. Из любой вершины выходит не более одного ребра, в отметке которого участвует каждый данный входной символ.
следует свойство графов, задающих конечные автоматы. Из любой вершины выходит не более одного ребра, в отметке которого участвует каждый данный входной символ.
Пример 6. Пусть на вход некоторого устройства поступают сигналы 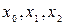 в любой последовательности. Устройство при
в любой последовательности. Устройство при
появлении на входе 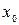 не изменяет выходной сигнал, а при появлении
не изменяет выходной сигнал, а при появлении 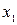 выдает на выходе
выдает на выходе 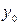 , а при появлении
, а при появлении 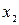 выдает
выдает 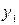 .
.
Представим этот процесс в виде конечного автомата у которого:
входной алфавит 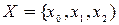 , выходной алфавит
, выходной алфавит 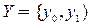 , алфавит состояний
, алфавит состояний 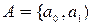 . Тогда граф автомата Мили будет иметь вид (рис. 9).
. Тогда граф автомата Мили будет иметь вид (рис. 9).
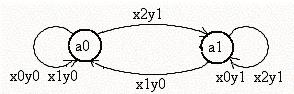
Рис.9
Задание автоматов таблицами переходов и выходов
Функции 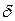 и
и 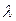 могут быть определены в виде общей таблицы переходов и выходов. Ее строки соответствуют различным входным символам из
могут быть определены в виде общей таблицы переходов и выходов. Ее строки соответствуют различным входным символам из 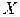 , а столбцы - различным символам из
, а столбцы - различным символам из 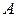 . В клетку таблицы, находящуюся на пересечении столбца с символом
. В клетку таблицы, находящуюся на пересечении столбца с символом 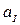 и строки с символом
и строки с символом 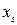 записывается пара
записывается пара 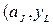 ),где
),где
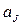 =
= 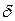 (
(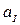 ,
, 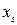 ),
), 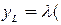
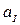 ,
, 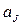 ,
, 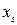 ).
).
Иногда эту таблицу представляют в виде двух таблиц - таблицы переходов и таблицы выходов, в которых аналогично общей таблице
строки и столбцы соответствуют символам из 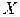 и
и 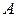 , а на пересечении столбца с символом
, а на пересечении столбца с символом 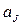 и строки символом
и строки символом 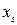 в таблице переходов записываются
в таблице переходов записываются 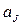 =
= 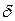 (
(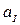 ,
, 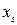 ), а в таблице выходов
), а в таблице выходов
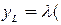
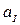 ,
, 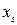 ).
).
Пример 7. Общая таблица переходов и выходов для автомата из примера (Рис. 9) имеет вид:
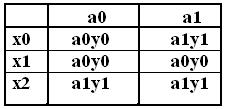
В случае автоматов второго рода таблицу выходов можно заменить на сдвинутую таблицу выходов, в которой на пересечении строки с символом 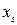 и столбца
и столбца 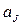 ставится символ
ставится символ 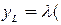
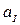 ,
, 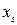 ). В случае автомата Мура сдвинутая таблица выходов сводится к одной строке и ее помещают над таблицей переходов, отметив тем самым каждое состояние автомата соответствующим ему выходным символом. Такую таблицу называют отмеченной таблицей переходов автомата Мура.
). В случае автомата Мура сдвинутая таблица выходов сводится к одной строке и ее помещают над таблицей переходов, отметив тем самым каждое состояние автомата соответствующим ему выходным символом. Такую таблицу называют отмеченной таблицей переходов автомата Мура.
|
|
|
Пример 8. Пусть задан автомат Мура графом (рис.10)
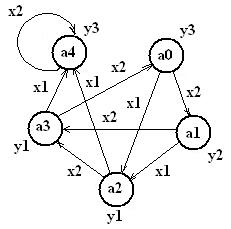
Рис.10
Его отмеченная таблица переходов
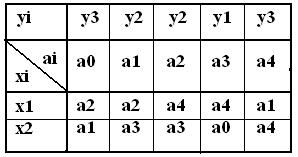
Для задания абстрактного автомата достаточно одной таблицы переходов, т.к. для него выходные символы совпадают с символами состояний.
Комбинационные схемы задаются только таблицей выходов (таблицей истинности).
 2015-07-21
2015-07-21 559
559








