Точность измерения координат целей является одной из важнейших характеристик РЛС, определяющих её возможности при решении задач целеуказания активным родам войск ПВО и ВВС и наведения истребителей.
Ошибка измерения представляет собой разность между истинным и измеренным значениями параметра 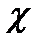 :
: 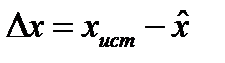 ,
,
где 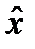 - измеренное значение (оценка) параметра.
- измеренное значение (оценка) параметра.
Ошибки измерений делятся на грубые промахи, систематические и случайные ошибки. Грубые и систематические ошибки в принципе можно устранить. Случайные ошибки можно минимизировать, но полностью устранить невозможно. Они обусловлены наличием помех на входе приемного устройства, его собственными шумами, флюктуациями сигнала, несовершенством выполнения и нестабильностями в элементах и устройствах РЛС.
Качественными показателями точности измерения координат целей, наиболее широко использующимися на практике, являются:
средняя квадратическая ошибка измерений 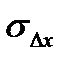 ;
;
срединная (вероятная) ошибка 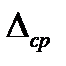 ;
;
ошибка в 80% измерений 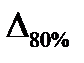 ;
;
максимальная ошибка 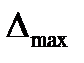 .
.
Средняя квадратическая ошибка при произвольном законе распределения плотности вероятности 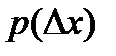 определяется из соотношения
определяется из соотношения
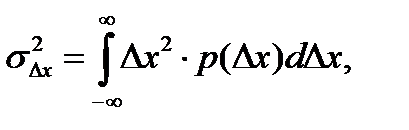 при
при 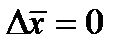 (3.6)
(3.6)
Условие 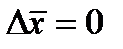 означает, что систематическая ошибка отсутствует, закон распределения ошибок в силу влияния множества факторов, обычно принимается нормальным
означает, что систематическая ошибка отсутствует, закон распределения ошибок в силу влияния множества факторов, обычно принимается нормальным 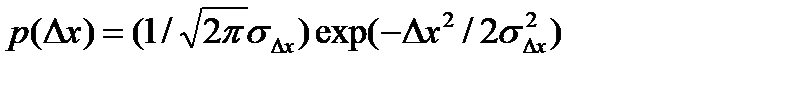 .
.
В этом случае средняя квадратическая ошибка пологостью характеризует другие виды ошибок. Вероятность того, что ошибка 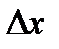 не превышает значения
не превышает значения 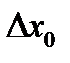 , равна
, равна
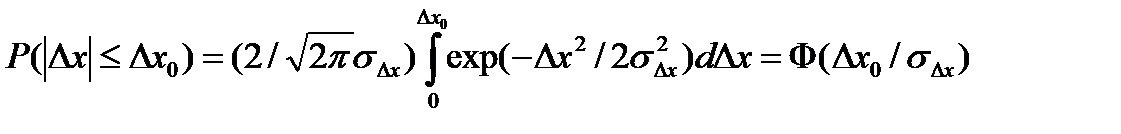 ,
,
где 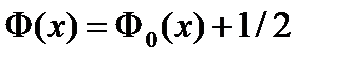 - гауссовский интеграл ошибок;
- гауссовский интеграл ошибок;
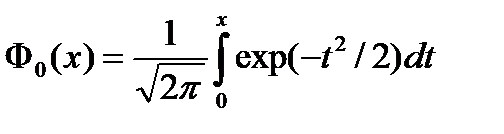 - табулированная функция (например, И.Н.Броншейн, К.А.Семендяев «Справочник по математике для инженеров и учащихся ВТУЗов» таблица 1.1.2.6.2).
- табулированная функция (например, И.Н.Броншейн, К.А.Семендяев «Справочник по математике для инженеров и учащихся ВТУЗов» таблица 1.1.2.6.2).
Количественное значение вероятности равно для:
срединной ошибки 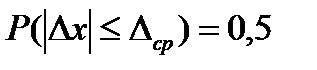 ;
;
средней квадратической ошибки 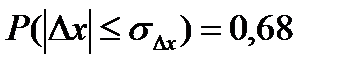 ;
;
ошибки в 80% измерений 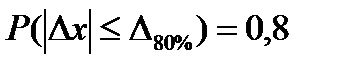 ;
;
максимальной ошибки 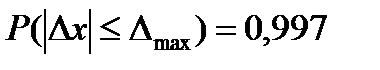 ;
;
Можно показать, что связь между ошибками определяется следующими соотношениями: 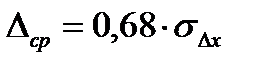 ;
; 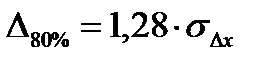 ;
; 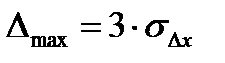 .
.
При цифровой обработке радиолокационные сигналы подвергаются дискретизации по времени и амплитуде, что приводит к дополнительным ошибкам измерения координат. Закон распределения ошибок дискретизации – равновероятный, т.е. плотность распределения вероятности ошибки 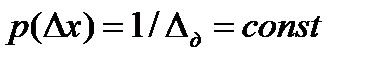 , где
, где 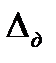 - шаг или интервал дискретизации.
- шаг или интервал дискретизации.
В соответствии с (3.6) средняя квадратическая ошибка дискретизации
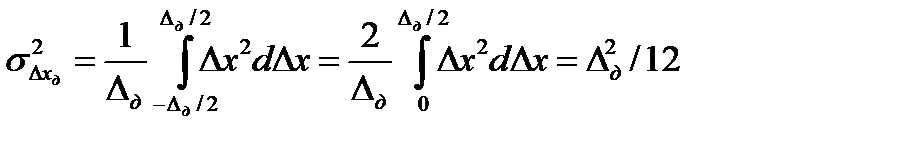 .
.
Откуда
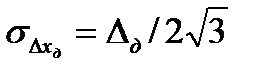 . (3.7)
. (3.7)
В общем случае средняя квадратическая измерения независимой координаты (дальности, азимута или угла места) определяется соотношением:
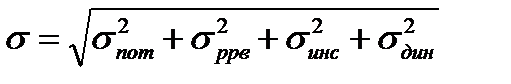 , (3.8)
, (3.8)
где 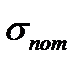 - потенциальная ошибка измерения координаты;
- потенциальная ошибка измерения координаты;
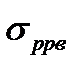 - ошибка, обусловленная особенностями распространения радиоволн в атмосфере;
- ошибка, обусловленная особенностями распространения радиоволн в атмосфере;
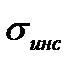 - инструментальная ошибка, обусловленная неидеальностью работы элементов и узлов РЛС, а так же способом измерения;
- инструментальная ошибка, обусловленная неидеальностью работы элементов и узлов РЛС, а так же способом измерения;
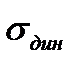 - динамическая ошибка, обусловленная изменением местоположения цели за время измерения.
- динамическая ошибка, обусловленная изменением местоположения цели за время измерения.
 2015-07-21
2015-07-21 1963
1963
