Декартова прямоугольная система координат

Для определения положения точки в пространстве мы будем использовать декартовы прямоугольные координаты (рис.2).

Декартова прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY, OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей. Ось OX называется осью абсцисс (или просто абсциссой), ось OY – осью ординат (ординатой), ось OZ – осью аппликат (апп ликатой).

Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки параллельно плоскостям YOZ, XOZ и XOY соответственно.

Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A.

Символически это записывают так:

A (x, y, z),

или

A = (x, y, z),

или привязывают запись координат к конкретной точке с помощью индекса:

x_A, y_A, z_A,

и т. п.

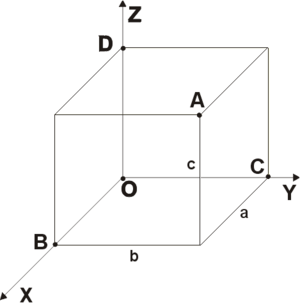
Рис. 2. Декартова прямоугольная система координат

Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче, приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка B лежала не как на рисунке — на луче OX, а на его продолжении в обратную сторону от точки O (на отрицательной части оси OX), то абсцисса x точки A была бы отрицательной (минус расстоянию OB). Аналогично и для двух других осей.

Координатные оси OX, OY, OZ, изображенные на рис. 2, образуют правую систему координат. Это означает, что если смотреть на плоскость YOZ вдоль положительного направления оси OX, то движение оси OY в сторону оси OZ будет проходить по часовой стрелке. Эту ситуацию можно описать при помощи правила буравчика: если буравчик (винт с правой резьбой) вращать по направлению от оси OY к оси OZ, то он будет двигаться вдоль положительного направления оси OX.

Векторы единичной длины, направленные вдоль координатных осей, называются координатными ортами. Их обозначают обычно как 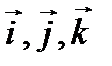(рис. 3). Встречается так же обозначение 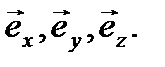Орты составляют базис координатной системы.

В случае правой системы координат действительны следующие формулы с векторными произведениями ортов:

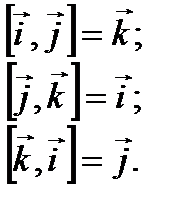
Положение точки в пространстве можно описать с помощью радиус-вектора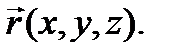

Радиус-вектор 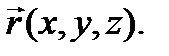– это вектор, проведенный из начала координат в точку, где находится тело (рис. 3.). Радиус-вектор можно разложить на составляющие:

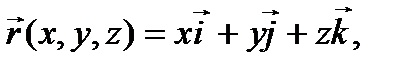
где 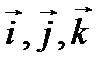— единичные векторы (орты), x, y, z – координаты точки.

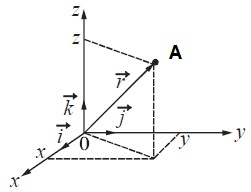
Рис. 3.

Базис декартовой прямоугольной системы координат