1. Знайти кількість вершин, ребер і степені кожної вершини неорієнтованих
графів:
а) 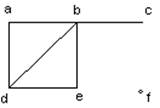 б)
б) 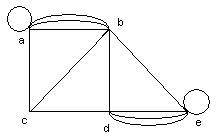
2. Знайти суму степенів вершин кожного з графів задачі 1 та переконатись, що вона вдвічі більша за кількість ребер графа.
3. Визначити кількість вершин та дуг і знайти напівстепені входу й виходу для кожної вершини орієнтованих графів:
а)  б)
б) 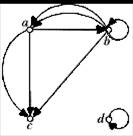
4. Для кожного з графів задачі 3 знайти суму напівстепенів входу та суму напівстепенів виходу вершин. Переконатись, що кожна з них дорівнює кількості дуг графа.
5. Побудувати графи:
а) К7; б) К1,8; в) К1,4; г) К3,4; д) С7; е) 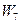 ; є)
; є) 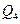
6. Які з наведених нижче графів дводольні?
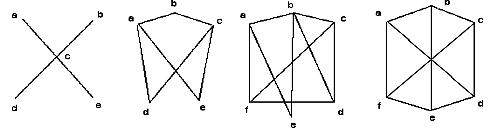
7. Для яких значень 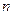 наведені нижче графи дводольні: а)
наведені нижче графи дводольні: а) 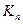 ; в)
; в) 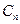 ; в)
; в) 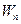 ; г)
; г) 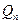 ?
?
8.  Скільки вершин і ребер мають наведені нижче графи: а)
Скільки вершин і ребер мають наведені нижче графи: а) 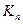 ; в)
; в) 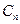 ; в)
; в) 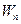 ; г)
; г) 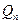 ; д)
; д) 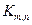 ?
?
9. Скільки ребер має граф, у якого вершини мають такі степені: 4, З, З, 2, 2? Зобразити його.
10. Чи існує простий граф із вершинами таких степенів? Якщо так, то зобразити його:
а) З, З, З, З, 2; б) 3, 4, 3, 4, 3; в) 1, 2, 3, 4, 5;
г) 1, 2, 3, 4, 4; д) 0, 1, 2, 2, 3; є) 1, 1, 1, 1, 1.
11. Нехай 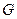 – граф з
– граф з 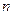 вершинами та
вершинами та 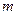 ребрами. Нехай
ребрами. Нехай 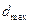 – максимальний степінь вершини цього графа, а
– максимальний степінь вершини цього графа, а 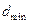 – мінімальний. Довести, що
– мінімальний. Довести, що 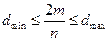 .
.
12. Що з переліченого нижче є шляхом у графі на мал. 1. Які з них є простими шляхами? Вкажіть довжину кожного шляху.
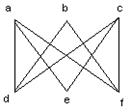 мал. 1
мал. 1
a) 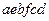 ;
;
b) 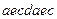 ;
;
c) 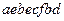 ;
;
d) 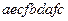 .
.
13. Що з переліченого нижче є шляхом у графі на мал. 2. Які з них є простими шляхами? Вкажіть довжину кожного шляху.
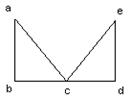 мал. 2
мал. 2
a) 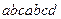 ;
;
b) 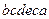 ;
;
c) 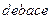 ;
;
d) 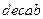 .
.
14. Знайдіть вершини й орієнтовані ребра для орграфів. Для кожної вершини визначте степінь входу й степінь виходу. Для кожного графа побудуйте чотири підграфа.
а) 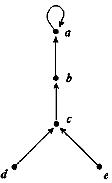 б)
б) 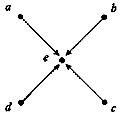 в)
в) 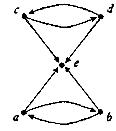 г)
г) 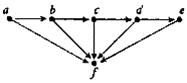
д) 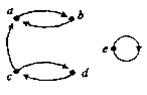 е)
е) 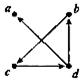 є)
є) 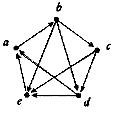 ж)
ж) 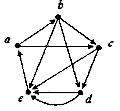
з) 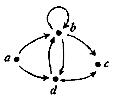 и)
и) 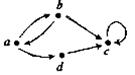 і)
і) 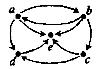 ї)
ї) 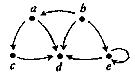
 2015-07-21
2015-07-21 643
643






