1. Побудувати бінарне дерево пошуку для слів banana, peach, pear, apple, coconut, mango, papaya.
2. Скільки потрібно порівнянь, щоб знайти чи додати кожне зі слів до дерева пошуку із задачі 1:
а) реаг, б) bаnаnа; в) plum; г) оrange.
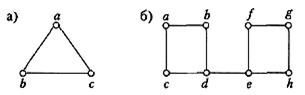
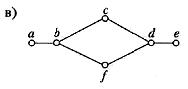
3. Використати бектрекінг для відшукання гамільтонових циклів у графах:
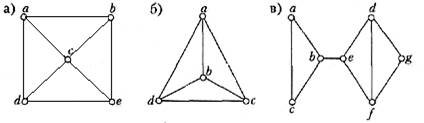
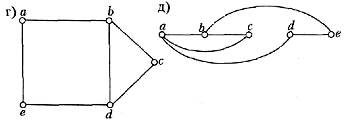
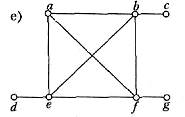
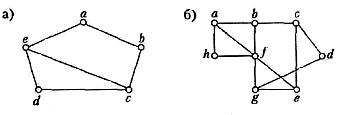
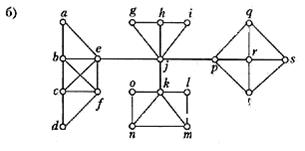
4. Використовуючи бектрекінг, розфарбувати в три кольори графи:
а) 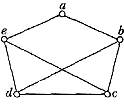 б)
б) 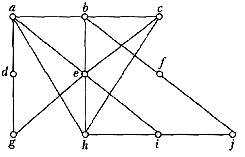
5. Використовуючи бектрекінг, розв'язати задачу про 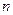 ферзів для значень
ферзів для значень 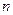 , що дорівнюють 3, 5 і 6.
, що дорівнюють 3, 5 і 6.
6. Використати бектрекінг для відшукання всіх максимальних незалежних множин вершин графів:
7. Використовуючи бектрекінг, знайти підмножину (якщо вона існує) множини {27, 24, 19, 14, 11, 8} із зазначеною сумою:
а) 20; б)41; в) 60.
8. Зв'язний граф 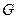 має
має 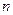 вершин і
вершин і 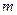 ребер. Скільки ребер потрібно вилучити з графа
ребер. Скільки ребер потрібно вилучити з графа 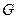 , щоб одержати каркас?
, щоб одержати каркас?
9. Знайти каркас для кожного з наведених нижче графів способом вилучення ребер із простих циклів.
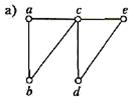
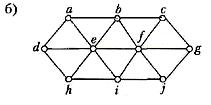
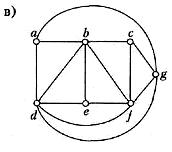
10. Побудувати каркаси для кожного з наведених нижче графів. Знайти цикломатичне число кожного графа:
а) 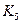 ; б)
; б) 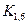 ; в)
; в) 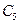 ; г)
; г) 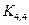 ; д)
; д) 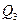 ; є)
; є)  .
.
11. Для простих графів побудувати всі можливі каркаси.
12. Довести теорему Келі: кількість позначених дерев з 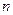 вершинами дорівнює
вершинами дорівнює 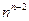 . Зазначимо, що всі позначені дерева з
. Зазначимо, що всі позначені дерева з 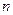 вершинами – це всі каркаси графа
вершинами – це всі каркаси графа 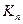 .
.
13. Зобразити всі позначені дерева з 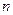 вершинами для значень
вершинами для значень 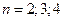 .
.
14. Скільки існує неізоморфних дерев з 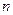 вершинами для значень
вершинами для значень 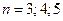 . Зобразити всі ці дерева.
. Зобразити всі ці дерева.
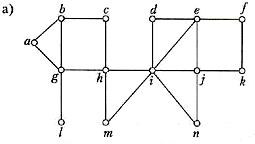
15. Використовуючи обхід графа пошуком углиб та вшир, побудувати каркаси для графів, наведених нижче. Як початкову вибрати вершину а.
 2015-07-21
2015-07-21 591
591






