ЭПР простых целей

Простейшей объемно распределенной целью являются дипольные отражатели, которые в большом количестве сбрасываются с самолета или выстреливаются специальными снарядами, рассеиваются в воздухе и образуют облако отражателей. Они применяются для постановки пассивных помех в широком диапазоне частот и одновременно против многих РТС.

Дипольные отражатели представляют собой пассивные полуволновые вибраторы с геометрической длиной, близкой к половине длины волны облучающей РЛС (l ≈ 0,47λ). Их изготавливают из металлизированной бумаги, алюминиевой фольги, металлизированного стекловолокна и других материалов.

ЭПР облака из n дипольных отражателей определяется произведением ЭПР отдельных отражателей, находящихся в облаке:

σ = n σ_do,

где: σ_do – ЭПР одного дипольного отражателя.

При линейной поляризации падающей электромагнитной волны максимальное значение ЭПР единичного дипольного отражателя наблюдается при совпадении его геометрической оси с вектором Е напряженности электрического поля волны. Тогда:

σ_{do max} = 0,86λ²

Если дипольный отражатель ориентирован перпендикулярно к вектору Е облучающей электромагнитной волны, то σ_do = 0.

Вследствие турбулентности атмосферы и различия аэродинамических свойств дипольных отражателей они ориентируются в облаке произвольно. Поэтому при расчетах используют среднее значение ЭПР единичного дипольного отражателя.

σ_{do sr} = 1/5 · σ_{do max} = 0,17λ²,

где: λ – длина волны облучающей РЛС.

Отсюда следует, что одновременное подавление РТС, работающих на различных частотах, возможно только при использовании дипольных отражателей различной длины.

Простейшей точечной целью являются уголковые отражатели. При относительно небольших геометрических размерах они обладают значительной величиной ЭПР в широком диапазоне длин волн, что позволяет эффективно имитировать различные точечные цели.

Уголковый отражатель состоит из жестко связанных между собой взаимно перпендикулярных плоскостей. Простейший уголковый отражатель представляет собой двугранный или трехгранный угол (рис.3.3,а,б).

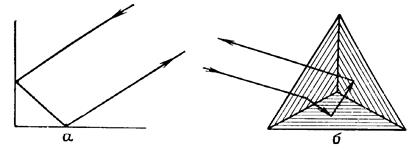
Рис.3.3. Принцип действия уголкового отражателя:

а – двугранного; б – трехгранного.

Трехгранный уголковый отражатель обладает свойством зеркального отражения в сторону РЛС при облучении в пределах угла 45⁰, что обеспечивает сохранение большой ЭПР в пределах этого угла. Для расширения диаграммы рассеяния применяют уголковые отражатели, состоящие из четырех или восьми уголков. ДР трехгранного отражателя показана на рис.3.4.

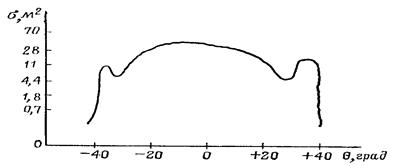
Рис.3.4. Диаграмма рассеяния трехгранного отражателя.

На практике используются трехгранные уголковые отражатели, имеющие треугольную, прямоугольную или секторную форму (рис.3.5,а,б,в).

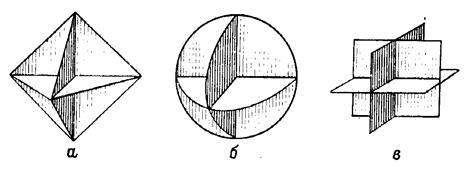
Рис.3.5. Уголковые отражатели: а – с треугольными гранями (θ_0,5 ≈ 60⁰);

б – с секторными гранями; в – с квадратными гранями (θ_0,5 ≈ 35⁰).

Для объектов простой геометрической формы можно получить аналитические выражения для определения их ЭПР. Так как плотность потока мощности прямо пропорциональна квадрату напряженности электрического поля, то формулу ЭПР цели можно представить в виде

σ = 4πD² · Е²₂/Е²₁

Отношение Е₂/Е₁, входящее в это выражение, можно найти на основании принципа Гюйгенса. Этот метод состоит в том, что каждая точка на поверхности облучаемого объекта рассматривается как источник вторичной сферической волны. Тогда, суммируя действие вторичных сферических волн в месте расположения РЛС, можно найти напряженность результирующего электрического поля вторичного излучения. Расчетные формулы для определения ЭПР некоторых простых целей приведены в табл.3.1.

Таблица 3.1. ЭПР некоторых простых целей.

Тип цели	Форма цели	Расчетная формула для ЭПР	Направление падающей волны
Шар		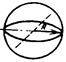πR2, при R» λ 144π4R6/λ4, при R < λ R – радиус шара	Произвольное
Круглый цилиндр		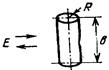2πRb2/λ, при 2πR/λ» 1	Падающая волна образует с осью цилиндра угол 900
Конус		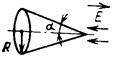λ2/16π · tg 4 α α– половинный угол конуса	Падающая волна совпадает с осью конуса
Плоский прямоугольный лист		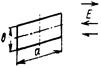4πS2/ λ2 S– площадь листа (S = ab)	Падающая волна образует с плоскостью листа угол 900
Уголковый отражатель с треугольными гранями		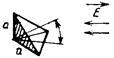4πa4/3 λ2 а – длина ребра отражателя	Падающая волна совпадает с максимумом диагр. рассеяния
Уголковый отражатель с прямоугольными гранями		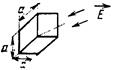12πa4/ λ2 а – длина ребра отражателя	Падающая волна совпадает с максимумом диагр. рассеяния
Дипольный отражатель (полуволновый вибратор)		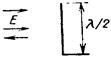0,86 λ2	Падающая волна образует с осью вибратора угол 900
Тип цели	Форма цели	Расчетная формула для ЭПР	Направление падающей волны
Сфероид		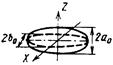4b04/a02 a0,b0– полуось сфероида	Падающая волна совпадает с полуосью a0 сфероида
Объект оживальной формы		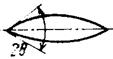λ2/16π ·tg4Θ Θ –половинный угол	Падающая волна совпадает с продольной осью объекта

В табл.3.1 приведена расчетная формула для ЭПР плоского листа при его облучении по нормали к поверхности. При отклонении направления облучения плоского листа от нормального облучения его ЭПР определяется иначе.

Например, рассматривая плоский прямоугольный лист длиной a и высотой b, как плоскую синфазную антенну с ДН, описываемой функцией:

E(x) = E_{m ,}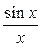

выражение для ЭПР плоского листа можно записать в виде:

σ = ,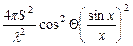

где: x = 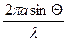, S = ab.

Отсюда следует, что при отклонении направления облучения плоского листа от нормального его ЭПР значительно уменьшается, а при некоторых углах облучения резко падает до 0. Большое значение ЭПР в достаточно широком секторе позволяют получить только уголковые отражатели.

Практическая ценность теоретических формул для определения ЭПР простых целей состоит в том, что при отсутствии экспериментальных данных они позволяют приближенно оценить ЭПР сложных целей.