Доказательство утверждения 2

Эквивалентность HS4 и GS4.

Утверждение 1.

├_HS4 F 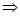├_GS4 → F

Утверждение 2.

├_GS4 Г →∆ 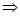├_HS4 (&Г) ()

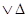Доказательство утверждения 1.

Индукцией по длине доказательства F₁,…, F_k формулы F в HS4.

Базис: k=1. F – аксиома.

Докажем, что все аксиомы HS4 доказуемы в GS4.

А0: каждая тавтология выводима по теореме о полноте для СКлИВ.

А1: □А А А→А

□ А→А

→ □А А

А2: □ (А В) (□А □В) А→А В→В

А В, А → В

□ (А В), А → В

□ (А В), □А → В

□ (А В), □А → □В

□ (А В) → (□А □В)

→□ (А В) (□А □В)

А3: □А □□А □А→ □А

□А→ □□А

→ □А □□А

Предположим для k<N утверждение доказано, докажем для k=N.

Пусть F_k доказывается по одному из правил вывода HS4.

а) правило МР:

А→А В→В

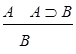
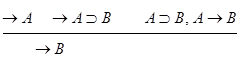
б) правило введение □:

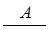
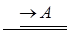
□ A →□ А.

Доказательство утверждения 2.

Доказательство ведем индукцией по длине доказательства S₁,…, S_k секвенции Г →∆ в GS4.

Базис: k=1. Секвенция имеет вид 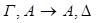. Заметим, что формула

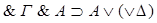является тавтологией, а, следовательно, и аксиомой HS4.

Предположим, что для k<N утверждение доказано. Докажем его для k=N.

Пусть S_k доказывается по одному из правил вывода GS4.

а) логические правила.

В качестве примера рассмотрим правило введение &. Остальные логические правила рассматриваются полностью аналогично.

1) & введение.

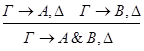
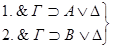доказываются по индукционному предположению,

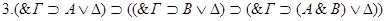тавтология КлИВ, аксиома А0,

4. 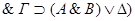два раза применяем правило МР (3,1,2).

2) модальные правила.

а) □ - удаление

Г,А→∆

Г, □А→∆

1. &Г &А ∆ доказуема по индукционному предположению,

2. □А А аксиома А1,

3. (&Г &А ∆) ((□ А А) (&Г &□ А ∆)) тавтология, аксиома А0,

4. &Г,& □А ∆, два раза применяем правило МР (3,1,2).

б) □ – введение

□Г→А

□Г→□А

1. &□Г А доказуема по индукционному предположению,

2. □ (&□Г А) по правилу □ – введение для HS4

3. □ (&□Г А) (□ (&□ Г) □ А) аксиома А2

4. □&□Г 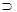□А по правилу МР из 2 и 3

5. &□□Г 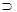□А по эквивалентности □(A&B) (□A & □B) в HS4

6. &□Г 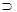□А по эквивалентности □□ А □А

что и требовалось доказать.