1) Если заряженная частица в магнитном поле движется вдоль линий магнитной индукции, то угол α между векторами v и B
равен 0 или π.Тогда сила Лоренца равна нулю
F=QvB 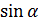 =
= 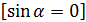 =0
=0
2) Если заряженная частица движется в магнитном поле со скоро-
стью, которая перпендикулярна вектору B,то
F=QvB 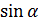 =
= 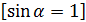 = QvB
= QvB
3) Частица будет дви-
гаться по окружности, радиус которой находится из условия
QvB= 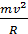 ,следовательно R=
,следовательно R= 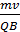 , а отношение
, а отношение 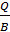 - удельный заряд частицы
- удельный заряд частицы
Период вращения частицы:T= 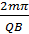
Ускорителями заряженных частиц называются устройства, которые под действием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных частиц. Ускорители подразделяются на непрерывные и импульсные. По форме траектории и механизму ускорения частиц ускорители делятся на линейные, циклические и индукционные.
Эффект Холла – это возникновение в металле или полупроводнике с током плотностью 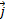 , который помещен в магнитное поле
, который помещен в магнитное поле 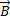 , электрического поля в направлении, перпендикулярном
, электрического поля в направлении, перпендикулярном 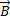 и
и 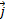 .
.
e 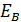 =
= 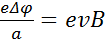 ,где
,где 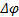 -поперечная разность потенциалов; а-ширина пластинки
-поперечная разность потенциалов; а-ширина пластинки
R 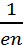 - постоянная Холла, которая зависит от вещества.
- постоянная Холла, которая зависит от вещества.
16.Циркуляция вектора 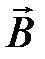 магнитного поля в вакууме. Магнитные поля соленоида и тороида.
магнитного поля в вакууме. Магнитные поля соленоида и тороида.
Циркуляция вектора магнитной индукции – интеграл по замкнутому контуру L проекции вектора магнитной индукции на направление обхода контура
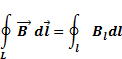
Теорема о циркуляции вектора индукции магнитного поля 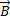 будет:
будет:
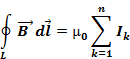
,где n – число проводников с токами.
Соленоид – цилиндрическая катушка, состоящая из большого числа витков, равномерно намотанных на сердечник.
Магнитная индукция внутри соленоида:B= 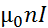
Вне соленоида: B=0
У конца полубесконечного соленоида, на его оси магнитная индукция равна :B= 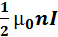
Магнитная индукция в произвольной точке внутри конечного соленоида: B= 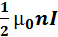 (
( 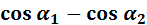 )
)
Тороид можно рассматривать как длинный соленоид, сверну-
тый в кольцо. Вне тороида магнитное
поле, создаваемое круговыми токами тороида, равно нулю.
B= 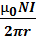 -магнитная индукция внутри тороида (в вакууме)
-магнитная индукция внутри тороида (в вакууме)
17. Поток вектора магнитной индукции. Теорема Гаусса для поля 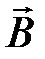 .
.
Потоком вектора магнитной индукции через площадку dS называется скалярная физическая величина, которая равна d 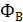 =
= 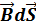 =
= 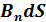
Теорема Гаусса для поля 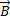 : поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:
: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю: 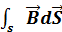 =
= 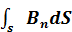 =0
=0
Эта теорема является отражением факта, что магнитные заряды отсутствуют, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми. Следовательно, для потоков векторов 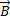 и
и 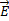 сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные формулы:
сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные формулы:
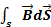 =
= 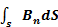 =0 и
=0 и 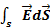 =
= 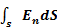 =
= 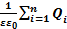
 2015-07-14
2015-07-14 3212
3212
