Формулировка и схема решения задачи рассеяния волн на сферической частице (на шаре).
Рассеяние оптических волн сферическими частицами полностью описывается строгими решениями уравнений Максвелла. Задача эта была решена Ми.
Учитывая симметрию рассеивающей частицы, уравнения Максвелла и граничные условия записываются в сферических координатах. Получается шесть уравнений в дифференциальной форме.
Граничные условия требуют непрерывности тангенциальных составляющих электрического и магнитного полей на поверхности сферы.
Второе – требуется достаточно быстрое убывание дифрагированных волн на бесконечности (принцип излучения).
Эта группа граничных условий исключает из рассмотрения сходящиеся волны, которые формально также удовлетворяют колебательным уравнениям.
Далее, чтобы получить решение уравнений Максвелла, вводятся скалярные потенциалы Дебая 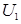 и
и 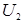 , однозначно связанные с составляющими электрического и магнитного полей (
, однозначно связанные с составляющими электрического и магнитного полей (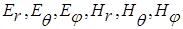 ).
).
Решение шести дифференциальных уравнений Максвелла после этого удается свести к решению одного волнового уравнения для электрического и магнитного полей (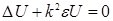 ).
).
После подстановки решений для потенциалов в соотношения, связывающие их с составляющими поля вне шара, дает искомые решения.
Запишем их для составляющих электрического поля
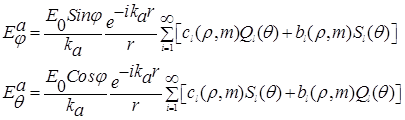
где  и
и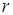 − сферические координаты;
− сферические координаты;
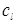 и
и 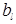 − амплитуды парциальных волн;
− амплитуды парциальных волн;
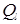 и
и 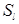 − угловые функции парциальных волн;
− угловые функции парциальных волн;
 − относительный показатель преломления;
− относительный показатель преломления;
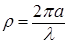 − параметр Ми,
− параметр Ми, 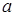 − радиус частицы,
− радиус частицы, 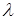 − длина волны.
− длина волны.
Составляющие для магнитных полей имеют аналогичный вид.
Радиальными составляющими полей в волновой зоне (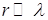 ) пренебрегаем, так как их убывание идет пропорционально
) пренебрегаем, так как их убывание идет пропорционально 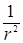 .
.
Условие
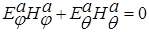
Выполняется для дифрагированных полей в целом и для каждой парциальной волны и означает их взаимную перпендикулярность.
Итак, теория Ми позволяет записать решение для дифрагированных составляющих полей и формулы для амплитуд и угловых функций парциальных волн. Этим исчерпывается математическое содержание задачи.
Следующая задача: с использованием этих решений и формул нам надо получить физически измеряемые величины.
1. В первую очередь нам необходимо знать интенсивность излучения, под которой понимается вектор Умова-Пойнтинга (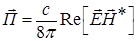 . Это средний по времени вектор потока электромагнитной волны на единичную площадку, нормальную к направлению распространения.
. Это средний по времени вектор потока электромагнитной волны на единичную площадку, нормальную к направлению распространения.
2. Для характеристики углового распределения интенсивности рассеянного излучения используется понятие индикатрисы рассеяния. Это отношение интенсивности рассеянного излучения к интегралу интенсивности по всем углам.
3. Для количественной характеристики энергетического ослабления вводится понятие коэффициентов рассеяния, поглощения и ослабления.
Под коэффициентом рассеяния понимается отношение суммарного потока электромагнитной энергии, рассеянной по всем направлениям, к интенсивности падающего потока. Размерность его м2, а поэтому называется сечением рассеяния.
Аналогично определяются коэффициенты поглощения и ослабления.
4. Кроме этого во многих случаях удобными характеристиками оказываются факторы эффективности рассеяния, поглощения, ослабления
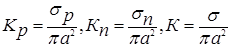
Как видим эти характеристики безразмерные.
Конкретные свойства коэффициентов рассеяния, поглощения и ослабления могут быть получены из расчетных и экспериментальных данных.
Рассмотрим, как ведет себя фактор эффективности ослабления в зависимости от параметра 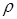 для
для 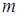 =1,33 и
=1,33 и 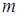 =
=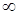 .
.
Рис.
Он, осциллируя, асимптотически приближается к значению 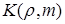 =2.
=2.
При больших значениях 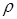 фактор эффективности ослабления
фактор эффективности ослабления 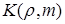 стремится к 2. А фактор эффективности рассеяния
стремится к 2. А фактор эффективности рассеяния 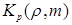 к единице (1), если частица поглощающая.
к единице (1), если частица поглощающая.
5. В общем случае, как мы убедились, расчеты по формулам Ми сложны.
Но есть два асимптотических случая, при которых формулы для
коэффициентов упрощаются до аналитических.
Это случай предельно малых частиц  1. Случай релевского рассеяния.
1. Случай релевского рассеяния.
В другом асимптотическом случае (предельно большие частицы) взаимодействие оптического излучения можно рассматривать как два независимых явления: 1) дифракцию волн на частице и
2) отражение и преломление лучей по законам геометрической оптики в частице.
Для описания дифракции волн в этом случае удается получить для суммарной интенсивности рассеянного вперед излучения формулу
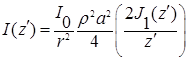
где 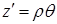 ;
; 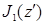 − функция Бесселя первого порядка.
− функция Бесселя первого порядка.
Эта формула точно совпадает с формулой для дифракции волн на круглом отверстии (для дифракции Фраунгофера) и показывает полную независимость интенсивности от электрических свойств частицы.
Границы применимости этой формулы определены: она справедлива для 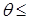 10○ и
10○ и 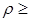 30.
30.
6. Интегрирование интенсивности рассеянного излучения по всем углам
определяет коэффициент рассеяния.
Проделав эту процедуру и отнеся полученную интенсивность к падающей, мы получим значение для коэффициента ослабления равное 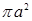 , а полный коэффициент ослабления при этом равен 2
, а полный коэффициент ослабления при этом равен 2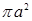 .
.
Следовательно, вторая половина коэффициента ослабления обуславливается рассеянием за счет отражения и преломления лучей частицей.
Этим объясняется парадокс, что полное сечение ослабления большой частицей равно ее двойному геометрическому сечению.
Следующая задача рассеяния, как обобщить теорию рассеяния оптического излучения отдельными частицами на систему частиц. Эта задача тоже не тривиальна.
Более просто она решается для случая однократного рассеяния. При этом если учитывать затухание интенсивностей падающего излучения до акта взаимодействия и рассеянного после акта взаимодействия, фактически учитывается многократное рассеяние.
Поэтому приближение однократного рассеяния с учетом затухания интенсивности в аэрозольной атмосфере называют первым приближением многократного рассеяния.
В общем же случае многократного рассеяния теория очень сложная.
При однократном рассеянии системой частиц считается, что частицы независимы. Поэтому фазовые соотношения рассеянных волн совершенно случайны (интерференция отсутствует) и без учета фазы складываются не амплитуды, а интенсивности рассеянных волн.
То есть, если интенсивность рассеянной волны 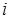 − й частицы
− й частицы 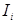 , то суммарная интенсивность определяется как
, то суммарная интенсивность определяется как
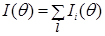 .
.
Интегрирование по всем направлениям рассеяния не изменяет это утверждение (соотношение), поэтому для коэффициента рассеяния системой частиц будем иметь
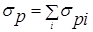 .
.
В направлении же вперед интерференция рассеянных волн может иметь место, так как при некотором расположении частиц может сохраняться соотношение фаз.
Следовательно, при очень малых углах рассеяния необходимо складывать амплитуды рассеянных волн.
Для суммарной амплитуды можно записать
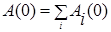 .
.
По оптической теореме ослабления величина 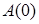 однозначно связана с коэффициентом ослабления и, следовательно, мы имеем
однозначно связана с коэффициентом ослабления и, следовательно, мы имеем
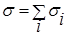 .
.
Вспомним, что такое оптическая теорема. Коэффициент ослабления через вектор Умова-Пойнтинга записывается как
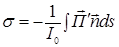 *
*
где 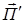 − поток, обязанный интерференции падающей и рассеянной волн.
− поток, обязанный интерференции падающей и рассеянной волн.
Если этот интеграл подсчитать, то можно получить
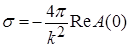 .
.
Это соотношение и носит название оптической теоремы.
* Нарисуем рассеивающую частицу. Окружим ее сферой. На частицу падает слева оптическое излучение. Коэффициент рассеяния будет
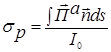 .
.
В случае, если частица поглощает, то 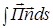 ˂ 0, тогда коэффициент поглощения будет
˂ 0, тогда коэффициент поглощения будет
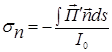 .
.
Общий поток при рассеянии на частице можно записать, как
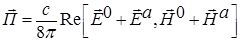 .
.
Тогда произведение 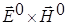 даст
даст 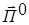 − поток падающего излучения.
− поток падающего излучения.
Произведение 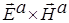 даст
даст  − поток дифрагированного поля.
− поток дифрагированного поля.
И появится поток, обязанный интерференции падающего и рассеянного излучений 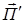 и получающийся перемножением вида
и получающийся перемножением вида 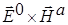 ,
,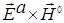 .
.
То есть 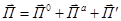 .
.
Запишем коэффициент ослабления 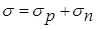
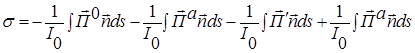
Первый член равен нулю (сколько энергии вошло в сферу, столько и вышло). Второй и четвертый уничтожаются. Остается
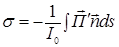
Теперь рассмотрим систему независимых рассеивателей как некоторый статистический ансамбль ослабителей для проходящего излучения. Статистический расчет (Раманхандран, 1960 г.) для системы из 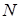 частиц приводит к формуле
частиц приводит к формуле
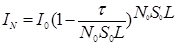
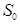 − поперечное сечение оптического пучка;
− поперечное сечение оптического пучка;
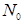 − концентрация частиц;
− концентрация частиц;
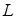 − длина трассы распространения;
− длина трассы распространения;
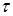 − оптическая толща.
− оптическая толща.
Эта формула представляет замечательный предел, который равен
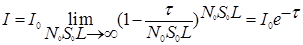 .
.
Это и есть экспоненциальный закон затухания. Он, как видим, выполняется только при большом числе рассеивателей 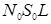 .
.
Этот закон, полученный раннее в поглощающих средах, известен под названием: закон Бугера.
Если единичный объем содержит 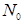 частиц с распределением частиц по размерам
частиц с распределением частиц по размерам 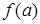 , то объемный коэффициент ослабления
, то объемный коэффициент ослабления 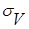 связан с коэффициентом ослабления отдельными частицами
связан с коэффициентом ослабления отдельными частицами 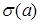 таким соотношением
таким соотношением
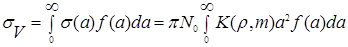
Аналогичная связь с сечением и для объемных коэффициентов рассеяния 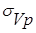 и поглощения
и поглощения 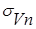 .
.
Из трех объёмных коэффициентов лишь два являются независимыми, так как
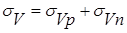 .
.
Иногда в задачах рассеяния используется величина
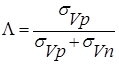 ,
,
которая называется вероятностью выживания кванта (или альбедо однократного рассеяния).
Таким образом, ослабление оптических волн в аэрозольной атмосфере полностью характеризуется двумя характеристиками, но только в случае изотропных частиц.
Если среда активная или анизотропная, тогда ослабление в ней описывается большим числом энергетических характеристик.
Третьей основной независимой характеристикой элементарного рассеивающего объема является индикатриса рассеяния.
Она также однозначно связана с индикатрисой рассеяния для отдельных частиц
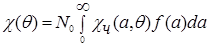 и нормирована
и нормирована 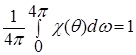 .
.
При учете поляризационных эффектов для системы частиц вместо индикатрисы рассеяния  необходимо ввести матрицу рассеяния, куда входит индикатриса рассеяния как элемент.
необходимо ввести матрицу рассеяния, куда входит индикатриса рассеяния как элемент.
Теперь нам остается уточнить, при каких условиях сохраняется независимость рассеяния.
Результаты теоретических оценок и экспериментальных исследований показывают, что эти условия сохраняются для малых рассеивателей 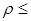 10 при расстояниях между частицами (4-6)
10 при расстояниях между частицами (4-6) 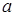 и более, а для больших рассеивателей
и более, а для больших рассеивателей 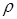 ≥10 при 10
≥10 при 10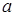 и более.
и более.
ОСОБЕННОСТИ РАССЕЯНИЯ МИ:
1. Сложная зависимость интенсивности рассеянного света от угла рассеяния (наблюдения).
2. Увеличение интенсивности рассеянного света в направлении вперед.
3. С ростом параметра Ми 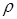 растет вытянутость индикатриссы рассеяния.
растет вытянутость индикатриссы рассеяния.
4. Слабая зависимость коэффициента рассеяния от длины волны 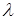 , когда
, когда 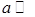
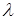 . Подтверждением этого служит белый цвет облаков.
. Подтверждением этого служит белый цвет облаков.
 2014-02-02
2014-02-02 1292
1292







