1. Доказать, что множество 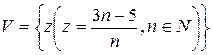 ограничено.
ограничено.
2. Дана последовательность с общим членом 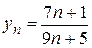 . Исполь-
. Исполь-
зуя первое и второе определение предела, а) доказать, что 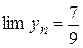 ; б) будет ли эта последовательность монотонной; в) найти sup yn и inf yn.
; б) будет ли эта последовательность монотонной; в) найти sup yn и inf yn.
3. Доказать, что функции y = sin x и y = tg x периодичны и определить их периоды.
4. При каких условиях параметрические уравнения
а) 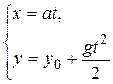 ; б)
; б) 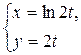 ; в)
; в) 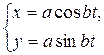 ; г)
; г) 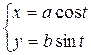
определяют функцию y = f (x)? Найти явный вид этих функций, а также уравнение F (x, y) = 0, с помощью которых эти функции заданы неявно.
5. Найти пределы функций:
1) 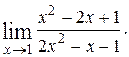 2)
2) 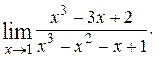 3)
3) 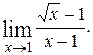
4) 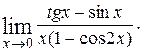 5)
5) 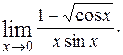 6)
6) 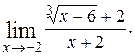
7) 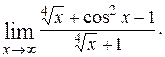 8)
8) 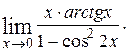 9)
9) 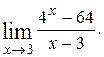
10) 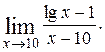 11)
11) 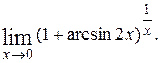 12)
12) 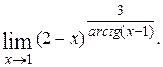
13) 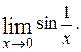 14)
14) 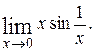
6. Исследовать следующие функции на непрерывность, найти точки разрыва и определить их характер, в точках устранимого разрыва доопределить функцию до непрерывности:
а) 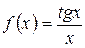 ; б)
; б) 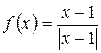 ; в)
; в) 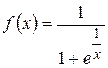 ; г)
; г) 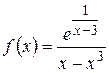 ; д)
; д) 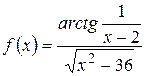 ; е)
; е) 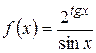 ; ж)
; ж) 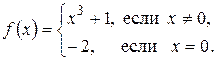
з) 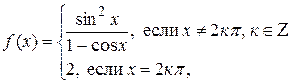 .
.
7. Определить естественную область определения функции и изобразить ее на плоскости:
а) 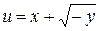 ; б)
; б) 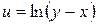 ; в)
; в) 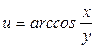 .
.
8. Используя метод сечения и линии уровней, построить график
функции
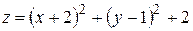 .
.
9. Для следующих функций найти точки разрыва и определить характер разрыва:
а) 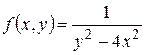 ; б)
; б) 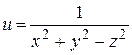 .
.
10. Найти производные следующих функций:
а) 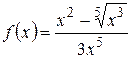 ; б)
; б) 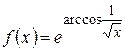 ; в)
; в) 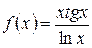 ;
;
г) 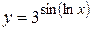 ; д)
; д) 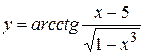 ; е)
; е) 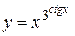 ;
;
ж) 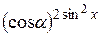 .
.
11. Найти уравнение касательной к кривой второго порядка 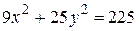 , проходящей через точку
, проходящей через точку 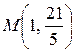 .
.
12. Пользуясь правилом Лопиталя, вычислить следующие пределы:
а) 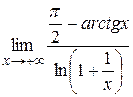 ; б)
; б) 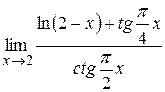 ; в)
; в) 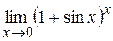 ;
;
г) 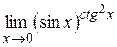 ; д)
; д) 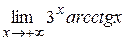 ; е)
; е) 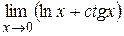 .
.
13. Используя формулу Тейлора, вычислить с точностью до 0,001 сле-
дующие значения:
а) 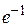 ; б)
; б) 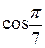 ; в)
; в) 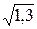 ; г)
; г) 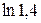 .
.
14.Найти наибольшее и наименьшее значения функций:
а) 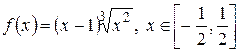 ; б)
; б) 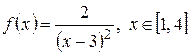 .
.
15. Определить наибольшую площадь прямоугольного треугольника,
вписанного в круг радиуса R.
16. Построить графики следующих функций:
а) 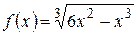 ; б)
; б) 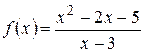 .
.
17. Найти полные дифференциалы функций:
а) 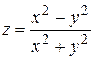 ; б)
; б) 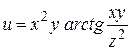 .
.
18. Найти частные производные функции 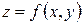 , заданной урав-
, заданной урав-
нением: а) 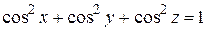 ; б)
; б) 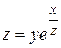 .
.
19. Найти вторые частные производные следующих функций:
а) 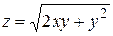 ; б)
; б) 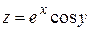 .
.
20. Найти наибольшее и наименьшее значение функции 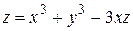 в прямоугольнике
в прямоугольнике 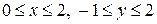 .
.
 2015-07-14
2015-07-14 244
244






