Производная логарифмической функции

Докажем формулу производной логарифмической функции для всех x из области определения и всех допустимых значениях основания a логарифма. По определению производной имеем:

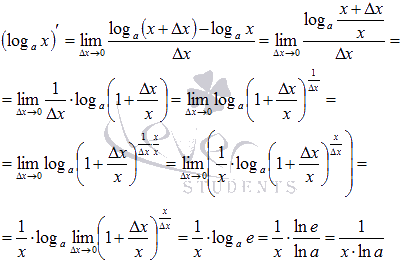
Как Вы заметили, при доказательстве преобразования проводились с использованием свойств логарифма. Равенство 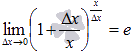справедливо в силу второго замечательного предела.

Пример.

Вычислить производные логарифмических функций .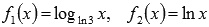

Решение.

Формулу мы уже вывели, так давайте ею и воспользуемся (в первом случае основание логарифма равно натуральному логарифму трех a = ln3, во втором a = e):

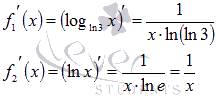
Таким образом, производная натурального логарифма равна единице деленной на x.