Метод вариации произвольной постоянной
(метод Лагранжа)
будем находить решение в виде 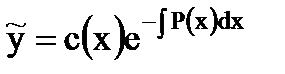 ,
,
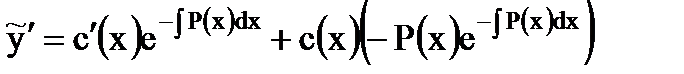 .
.
Для ее нахождения подставим 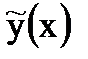 и
и 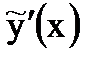 в уравнение (1.11). Поскольку
в уравнение (1.11). Поскольку
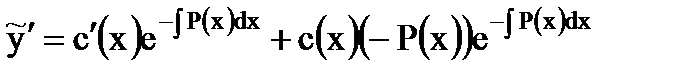 ,
,
то подстановка 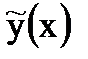 и
и 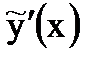 в (1.11) приводит к уравнению
в (1.11) приводит к уравнению
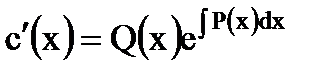 .
.
Проинтегрировав это уравнение, получим
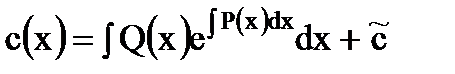 ,
, 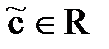 .
.
Итак, общее решение линейного неоднородного уравнения (1.11) имеет вид
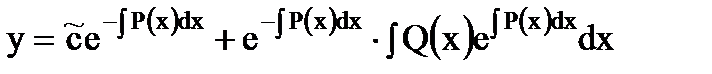 .
.
Метод Бернулли
Будем искать решение уравнения (1.11) как произведение двух функций: 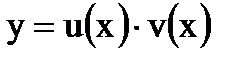 . Дифференцируя обе части равенства, получаем
. Дифференцируя обе части равенства, получаем 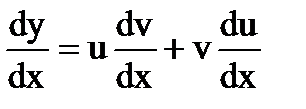 . Подставив
. Подставив 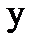 и
и 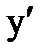 в уравнение (1.11), будем иметь
в уравнение (1.11), будем иметь 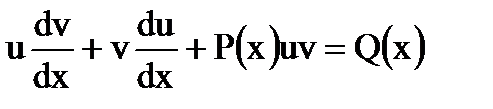 или
или
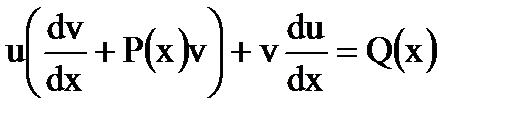 . (1.13)
. (1.13)
Поскольку необходимо найти две функции 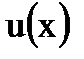 и
и 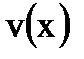 , а уравнение для их нахождения одно – (1.13), то выберем функцию v так, чтобы
, а уравнение для их нахождения одно – (1.13), то выберем функцию v так, чтобы 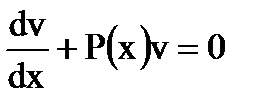 .
.
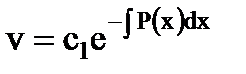 ,
, 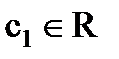 .
.
.Функцию 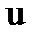 найдем из уравнения
найдем из уравнения 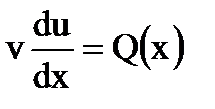 , которое получается из (1.13) при условии
, которое получается из (1.13) при условии 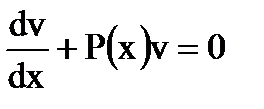 , т.е.
, т.е.
при 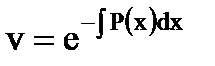 .
.
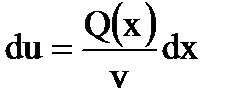 ,
,
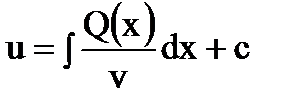 .
.
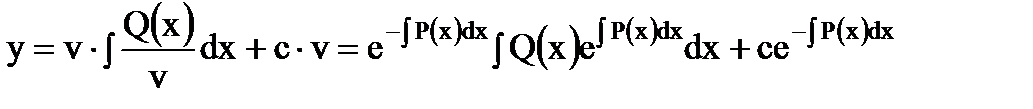 ,
,
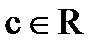 .
.
 2015-07-21
2015-07-21 277
277







