Квадратное уравнение
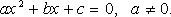
Дискриминант: 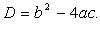
Если D > 0, то кв. ур-е имеет два различных корня: 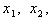 которые могут быть вычислены по формулам:
которые могут быть вычислены по формулам:
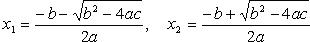
или
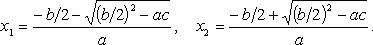
Если D = 0, то кв. ур-е имеет единственный корень 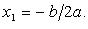 . Если D < 0, то действительных корней нет.
. Если D < 0, то действительных корней нет.
Частные случаи
1. 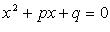 (приведенное квадратное уравнение),
(приведенное квадратное уравнение), 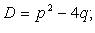
при D > 0
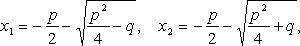
при D = 0
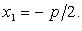
2. 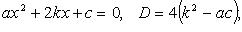
при D > 0
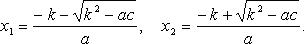
при D = 0
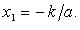
3. 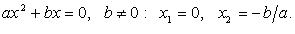
4. 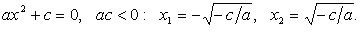
5. 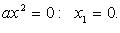
Связь между коэффициентами и корнями квадратного уравнения (формулы Виета)
Если 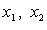 - корни квадратного уравнения
- корни квадратного уравнения 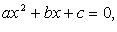 то
то
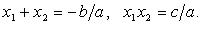
Для уравнения 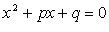
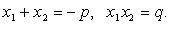
Разложение квадратного трехчлена на множители
Если D > 0, то 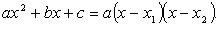
Если D = 0, то 
Квадратичные неравенства
D - дискриминант, 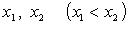 - корни квадратного уравнения
- корни квадратного уравнения 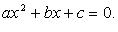 .
.
1. 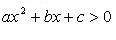 .
.

2. 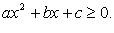 .
.

Неравенства 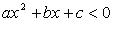 и
и 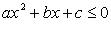 сводятся к рассмотренным умножением на -1.
сводятся к рассмотренным умножением на -1.
Частные случаи

Биквадратное уравнение
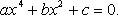
Сводится к квадратному уравнению заменой 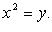
 2015-07-21
2015-07-21 491
491






