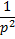Уравнение Эйлера, для нахождения 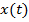 доставляющих экстремум функционалу
доставляющих экстремум функционалу
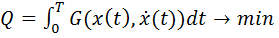 (1)
(1)
имеет вид
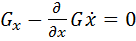 (2)
(2)
где 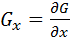 ,
, 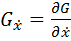 .
.
В большинстве технических задач вариационного исчисления функции доставляющие экстремум (1) подчинены уравнениям объекта, т.е.
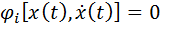
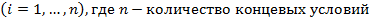
Для решения вариационной задачи используют метод неопределенных множителей Лагранжа. Суть этого метода состоит в том, что уравнение Эйлера (2) составляется для вспомогательных функций
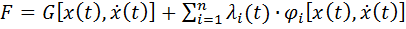 (3)
(3)
где 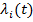 - множители Лагранжа, подлежащие определению; i=1,…,m; m=n-2.
- множители Лагранжа, подлежащие определению; i=1,…,m; m=n-2.
Если условия, которым подчинены искомые функции, заданы в виде
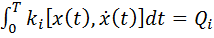 (4)
(4)
где 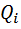 - заданные величины, то для решения задачи так же создаются вспомогательные функции.
- заданные величины, то для решения задачи так же создаются вспомогательные функции.
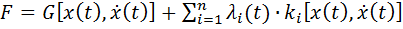 (5)
(5)
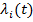 не зависят от времени.
не зависят от времени.
Пример:
Разворот искусственного спутника Земли на заданный угол:
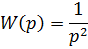
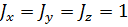
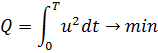
Начальные и конечные скорости нулевые:
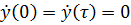 (2)
(2)
Уравнение объекта
|

 u y
u y
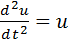 (1)
(1)
Задана величина отбрасываемого угла:
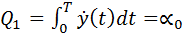 (3)
(3)
Введем обозначения:
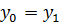 ¾ угол
¾ угол
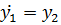 ¾ угловая скорость →
¾ угловая скорость → 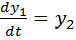
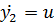 ¾ ускорение
¾ ускорение
Тогда (I), (II), (III) можно переписать слeдующим образом:
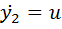 (4)
(4)
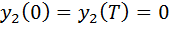 (5)
(5)
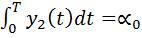 (6)
(6)
Функционал, который нужно минимизировать выбором функции 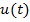 и
и 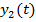 , является
, является
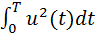 или с учетом (4)
или с учетом (4)
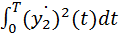 (7)
(7)
Подынтегральная функция в минимальном функционале 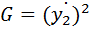 ,
,
а значение которого задано 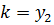 .
.
Образуем функцию F:
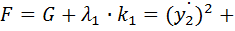
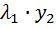 (8)
(8)
Составим уравнение Эйлера:
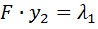
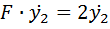
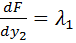
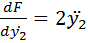
Окончательно имеем
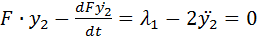 или
или
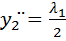 (9)
(9)
Проинтегрируем (9)
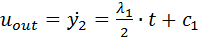 (10)
(10)
Это закон изменения управляющего воздействия.
Повторно интегрируем (10). Найдем оптимальный процесс
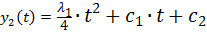 (11)
(11)
В принципе задача решена, но для нахождения 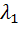 ,
, 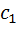 ,
, 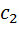 воспользуемся уравнениями (5) и (6).
воспользуемся уравнениями (5) и (6).
Подставим в (11) 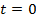 , имеем
, имеем
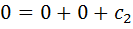 →
→ 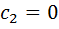
Подставим в (11) 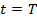 , имеем
, имеем
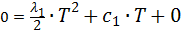 (12)
(12)
Из (11):
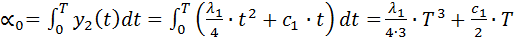 (13)
(13)
Из (12) и (13) имеем
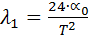
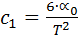
Окончательно можно записать
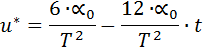
(14)
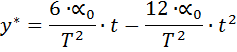
Графики, соответствующие (14), имеют вид
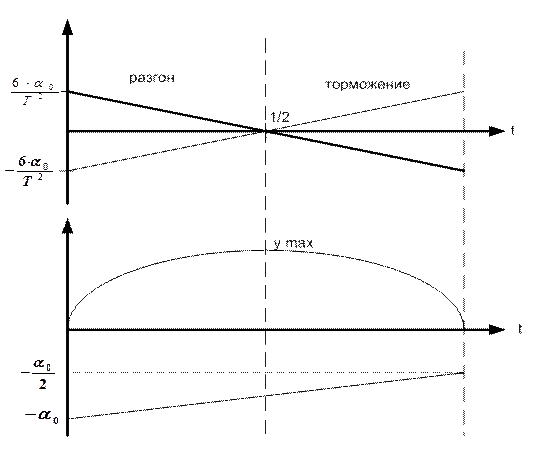
После 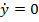 отходим от нужного угла в положительную сторону. Т.е. получим программный режим.
отходим от нужного угла в положительную сторону. Т.е. получим программный режим.
 2015-07-21
2015-07-21 126
126