II. Тригонометрические неравенства

Основной способ решения тригонометрических неравенств состоит в их сведении к неравенствам вида

sin x Ú a, cos x Ú a, tg x Ú a, ctg x Ú a,

(1)

где a Î R, символ "Ú" означает знак сравнения и заменяет любой из знаков ">", " ≥ ", "<", " ≤" и использовании следующих утверждений.

Утверждение 1. Множество решений неравенства

sin x > a

(2)

есть

1. R, если a < -1;
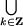2. (arcsin a + 2p k; p - arcsin a + 2p k), если -1 ≤ a < 1;
3. Пустое множество, если a ≥ 1.

Утверждение 2. Множество решений неравенства

sin x < a

(3)

есть

1. R, если a > 1;
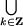2. (-p - arcsin a + 2p k; arcsin a + 2p k), если -1 < a ≤ 1;
3. Пустое множество, если a ≤ -1.

Утверждение 3. Множество решений неравенства

cos x > a

(4)

есть

1. R, если a < -1;
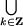2. (2p k - arccos a; 2p k + arccos a), если -1 ≤ a < 1;
3. Пустое множество, если a ≥ 1.

Утверждение 4. Множество решений неравенства

cos x < a

(5)

есть

1. R, если a > 1;
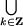2. (2p k + arccos a; 2p(k + 1) - arccos a), если -1 < a ≤ 1;
3. Пустое множество, если a ≤ -1.

Утверждение 5. Множество решений неравенства

tg x > a

(6)

есть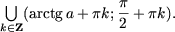

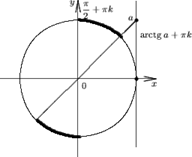
Утверждение 6. Множество решений неравенства

tg x < a

(7)

есть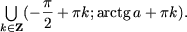

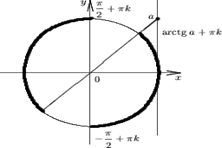
Утверждение 7. Множество решений неравенства

ctg x > a

(8)

есть 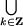(p k; arcctg a + p k).

Утверждение 8. Множество решений неравенства

ctg x < a

(9)

есть 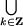(arcctg a + p k; p(k + 1))

Замечания. 1. Если знак неравенства (2)-(9) нестрогий, то во множестве решений неравенства включается также и множество решений соответствующего уравнения.