2015-07-21
135Линией второго порядка называется множество точек плоскости, координаты которых удовлетворяют уравнению:
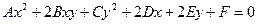
где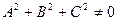 
(если коэффициенты А, В, С одновременно буду равны нулю, то уравнение преобразуется в уравнение первого порядка, то есть в уравнение прямой).
Дискриминант уравнения: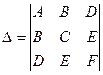 
; дискриминант старших членов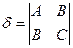 
В зависимости от значений 
и δ уравнение и имеет разный геометрический образ:
| 
| |
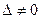
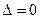
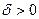
| Эллипс (действительный или мнимый) | Точка |
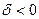
| Гипербола | Пара пересекающихся прямых |
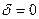
| Парабола | Пара параллельных прямых (действительных или мнимых) |
Примеры:
| № | Соответствие коэффициентов | Каноническое уравнение | Название |
| 
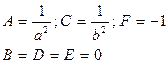
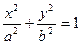
| Эллипс | |
| 
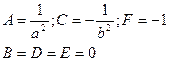
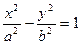
| Гипербола | |
| 
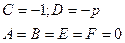
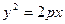
| Парабола | |
| 
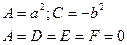
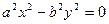
| Уравнение двух пересекающихся прямых | |
| 
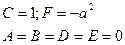
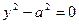
| Уравнение двух параллельных прямых | |
| 
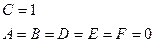
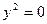
| Уравнение двух совпадающих прямых | |
| 
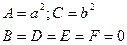
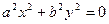
| Одна точка (0,0) | |
| 
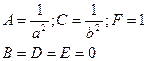
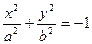
| Уравнение пустого множества (мнимый эллипс) | |
| 
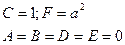
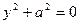
| Уравнение пустого множества (две мнимые параллельные прямые) |
