Период – время одного полного оборота.
Заметка: период секундной стерлки Т=1мин, период минутной стрелки Т=1час, период часовой стрелки Т=12часов.
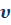 - Частота (Гц)
- Частота (Гц)
Частота – это число оборотов за единицу времени.
Период и частота – обратные величины.
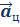 - Центростремительное (нормальное) ускорение (м/c2)
- Центростремительное (нормальное) ускорение (м/c2)
Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости. Центростремительное ускорение в любой точке траектории направлено по радиусу к центру окружности.
Формулы для равномерного движения по окружности:
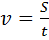 (17.)
(17.) 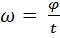 (18.)
(18.)
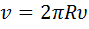 (19.)
(19.) 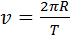 (20.)
(20.) 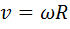 (21.)
(21.)
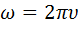 (22.)
(22.) 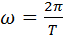 (23.)
(23.)
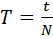 (24.)
(24.) 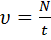 (25.)
(25.) 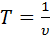 (26.)
(26.)
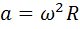 (27.)
(27.) 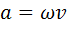 (28.)
(28.) 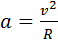 (29.)
(29.)
Здесь: S – путь (м.), t – время (сек.),  – линейная скорость (м/с), φ – угол поворота радиуса (рад), ω – угловая скорость (рад/сек), R – радиус (м), υ – частота (Гц = сек-1), Т – период (сек.), N – число оборотов (безразм.), а – центростремительное ускорение (м/с2).
– линейная скорость (м/с), φ – угол поворота радиуса (рад), ω – угловая скорость (рад/сек), R – радиус (м), υ – частота (Гц = сек-1), Т – период (сек.), N – число оборотов (безразм.), а – центростремительное ускорение (м/с2).
Пример: пусть имеется вращающийся вал, радиус которого R = 4,2м. Расстояния от центра вала до точек А, В и С указаны на рисунке. Так же нам известно, что период точки А: 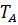 = 60 секунд.
Найдем периоды, частоты, угловые и линейные скорости точек А, В и С, = 60 секунд.
Найдем периоды, частоты, угловые и линейные скорости точек А, В и С,
|
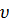 , и угловую скорость, но разные линейные скорости. Чем ближе точка на радиусе к центру окружности, тем менше ее линейная скорость.
, и угловую скорость, но разные линейные скорости. Чем ближе точка на радиусе к центру окружности, тем менше ее линейная скорость.
| A |
| B |
| C |
| 1 м |
| 2 м |
| 4 м |
| O |
Для точки А: Зная период Т, можем найти частоту по формуле (26):
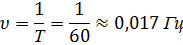 Так же найдем угловую скорость ω точки А по формуле (23):
Так же найдем угловую скорость ω точки А по формуле (23):
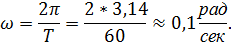 Точки А В и С имеют одинаковые период, частоту и угловую скорость.
Точки А В и С имеют одинаковые период, частоту и угловую скорость.
|
Значит: 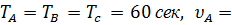 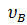 = = 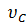 = 0,017 Гц, = 0,017 Гц, 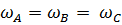 = 0, 1 рад/сек.
Найдем линейные скорости точек из формулы (21): = 0, 1 рад/сек.
Найдем линейные скорости точек из формулы (21):
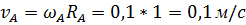
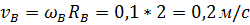
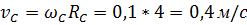 Мы видим, что не смотря на то что угловые скорости точек одинаковы, их линейные скорости различны.
Мы видим, что не смотря на то что угловые скорости точек одинаковы, их линейные скорости различны.
|
Утверждение о том, что период не зависит от радиуса покажется очевидным если мы вспомним о том, что вне зависимости от размеров часов (их радиуса) все секундные, например, стрелки имеют одинаковый период Т = 1 мин, т.е. совершают полный оборот за минуту.
 2015-08-21
2015-08-21 599
599







