Транспортная задача

Индивидуальное задание.

Решить систему уравнений тремя способами: методом Гаусса, по формулам Крамера и с помощью обратной матрицы.

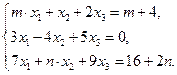
Исследовать и решить системы уравнений.

1.

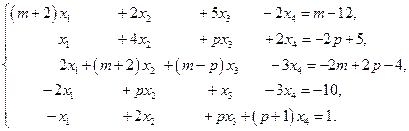
2.

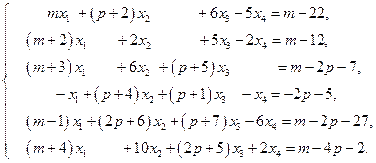
3.

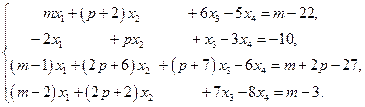
Дополнительное задание.

Исследовать и решить системы уравнений.

1.

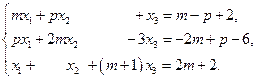
2.

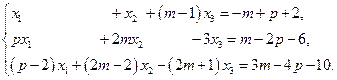
3.

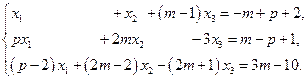
Линейное программирование

Следующие задачи лин. программирования решить графическим способом.

1.

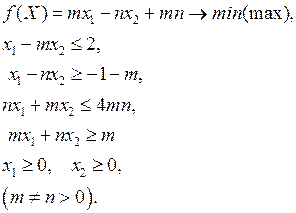
2.

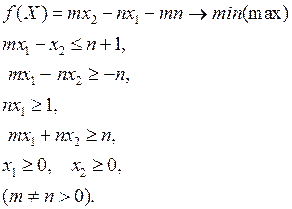
3.

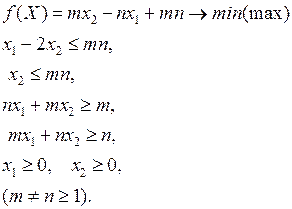
4.

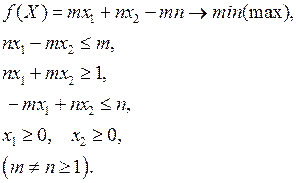
Транспортная задача

Рассмотрим транспортную задачу, т. е. задачу, в которой речь идет о рациональной перевозке некоторого однородного продукта (например, телевизоров) со складов в магазины. Пусть имеется m складов и n магазинов. Мощности (объемы) складов составляют а_i 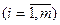единиц однородного продукта, а потребности каждого j -го магазина равны 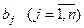единиц. Известны затраты 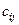на перевозку единицы продукта с i -го склада в j -й магазин. Матрицу 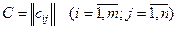называют матрицей затрат (тарифов).

Требуется составить такой план перевозок, при котором суммарные затраты на все перевозки были бы наименьшими. Пусть спрос и предложение совпадают, т.е. 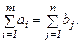Такую транспортную задачу называют сбалансированной (закрытой). При этом предполагается, что вся продукция со складов будет вывезена и спрос каждого из потребителей (магазинов) будет удовлетворен.

Составим математическую модель задачи. Обозначим через 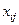- количество продукта, перевозимого с i -го склада в j -й магазин. Тогда матрица 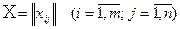называется планом перевозок.

Внесем исходные данные и перевозки 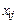в транспортную таблицу:

bj ai	b1	b2	...	bn
a1	c11 x11	c12 x12	...	c1n x1n
a2	c21 x21	c22 x22	...	c2n x2n
...	...	...	...	...
am	cm1 xm1	cm2 xm2	...	cmn xmn

Предположим, что транспортные затраты прямо пропорциональны количеству перевозимого продукта. Тогда суммарные затраты выразятся функцией цели (целевой функцией):

,

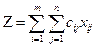которую необходимо минимизировать при ограничениях:

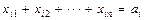
(весь продукт из каждого i -го 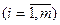пункта должен быть вывезен полностью),

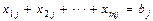
(спрос каждого j -го 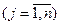потребителя должен быть полностью удовлетворен).

Из условия задачи следует, что все

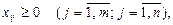
а иногда даже представляют собой целые числа (как, например, телевизоры).

Итак, математическая модель сбалансированной транспортной задачи имеет вид:

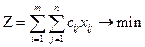
при ограничениях (ОДР):

.

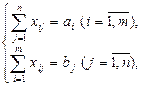
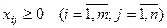В качестве индивидуального задания надо решить сбалансированную транспортную задачу, задав самостоятельно количество складов и магазинов (примерно 3,4), матрицу тарифов перевозок, мощности (объемы) складов и требования магазинов.