Бинарное дерево поиска на множестве NR ключей есть бинарное дерево TNR, в котором каждая вершина помечена отдельным ключом и расположена в соответствии с определенным порядком ключей. Для любой вершины i ключи вершин в его левом поддереве «меньше» ключа вершины i, который, в свою очередь, «меньше» ключей вершин в его правом поддереве.
Введем следующие обозначения:
Пусть k* определяет ключ элемента, находящегося в корне дерева, Л = {ki} – множество ключей, размещенных в вершинах левого поддерева, и П = {ki} – множество ключей, размещенных в вершинах правого поддерева.
Тогда для двоичного дерева поиска устанавливаются следующие правила размещения элементов:
(a) Для любого ki 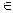 Л ki < k*;
Л ki < k*;
(b) Для любого ki 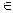 П ki > k*.
П ki > k*.
Указанные соотношения применяются к любому поддереву внутри двоичного дерева.
Пример двоичного дерева поиска приведен на рис. II-43.
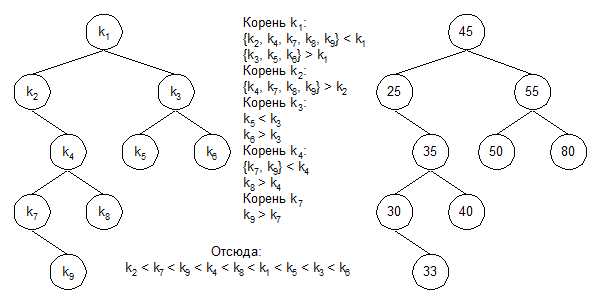
Рис. II‑43.
Для того чтобы получить действительно упорядоченный по возрастанию ключей список значений элементов, нужно использовать обратный обход дерева (ЛКП); в результате его применения к дереву, представленному на рис. II-43, получим:
25, 30, 33, 35, 40, 45, 50, 55, 80.
При анализе алгоритма поиска определяют длину пути до целевой записи как количество просмотренных вершин дерева от корня до целевой вершины.
Введем некоторые определения.
1. Уровень вершины или листа i, обозначаемый Li, определяется длиной пути от корневой вершины TNR до вершины i.
Корневая вершина, по определению, имеет уровень 0.
2. Высота дерева определяется как максимальный уровень среди всех вершин дерева.
3. Бинарное дерево называется сбалансированным, если разница уровней любых двух листьев не превышает 1.
Использование сбалансированного дерева минимизирует среднюю длину доступа.
Неудобство бинарных деревьев поиска заключается в том, что они слишком «высокие»; требуется просмотреть достаточно большое количество вершин дерева, прежде чем будет найдена искомая.
Для того чтобы найти в двоичном дереве элемент по значению его ключа, используются сформулированные выше правила, в соответствии с которыми, если искомый ключ меньше ключа в вершине дерева, следует продолжить просмотр левого поддерева; если больше – правого. Поиск в поддереве выполняется так же, как и в дереве (в силу рекурсивности определения двоичного дерева). Алгоритм поиска элемента в двоичном дереве приведен на рис. II-44.
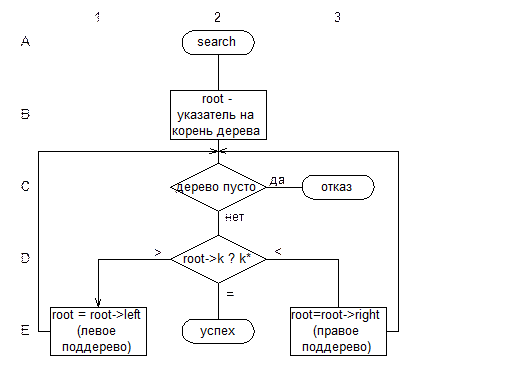
Рис. II‑44.
Здесь root->k определяет ключ элемента, root->left – указатель на левое поддерево, root->right – указатель на правое поддерево дерева, корень которого задается указателем root.
Текст функции приводится ниже.
struct Node{
int key;
Node *left, *right;
};
Node *search(Node *root, int k)
{
while(root && root->key!= k)
root = k < root->key? root->left: root->right;
return root;
}
В силу рекурсивного определения дерева функцию поиска элемента можно также реализовать как рекурсивную; текст рекурсивной функции приводится ниже.
Node *recsearch(Node *root, int k)
{
if(!root)
return NULL; /* элемент с указанным ключом отсутствует */
return (root->key == k)? root:
(k < root->key)? recsearch(root->left, k):
recsearch(root->right, k);
}
Однако, реализация рекурсивного алгоритма поиска не оправданна, что можно увидеть из анализа и сравнения приведенных текстов.
Учитывая, что операция поиска обычно предшествует операциям вставки и удаления, рассмотрим еще один вариант реализации поиска в двоичном дереве, в котором используется тип данных «указатель на указатель на …». В этом варианте, если поиск завершается успешно, функция возвращает указатель на поле, в котором хранится указатель на найденный элемент дерева. Если же поиск завершается не успешно, функция возвращает указатель на поле, в котором находится значение NULL.
Текст функции приводится ниже.
Node **find(Node *root, int k)
{
Node **pptr = &root;
while(*pptr && (*pptr)->key!= k)
pptr = k < (*pptr)->key? &(*pptr)->left: &(*pptr)->right;
return pptr;
}
Вставка в бинарное дерево проста: продвигаясь по соответствующим (в зависимости от значения ключа нового элемента) поддеревьям, находим вершину, имеющую в требуемом поле указателя на поддерево значение NULL, и к этому элементу подсоединяем новый элемент. При этом можно получить разные формы дерева – от линейного списка (Рис. II-45, а) до сбалансированного дерева (Рис. II-45, б). Наиболее часто встречается нечто среднее между этими двумя крайними случаями (Рис. II-45, в).
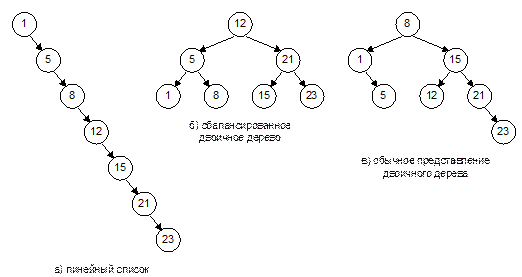
Рис. II-45.
Схема алгоритма включения нового элемента в двоичное дерево приведена на рис. II-46.
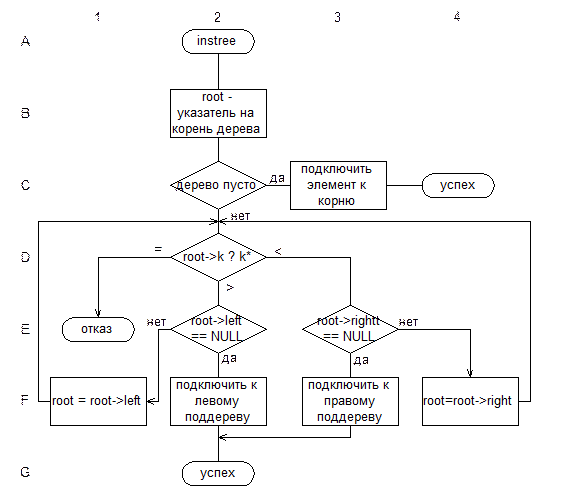
Рис. II‑46.
Функцию включения нового элемента можно сократить, если:
(a) использовать тип данных "указатель на указатель на...";
(b) использовать рекурсию.
Рассмотри оба способа реализации функции.
В варианте (a) использование типа "указатель на указатель на элемент дерева" позволяет объединить идентичные операции по включению нового элемента в левое или правое поддерево. Текст функции приводится ниже. Функция возвращает NULL, если элемент не может быть включен в таблицу (элемент с таким ключом в таблице уже есть или нет памяти для построения нового элемента дерева), и указатель на новый элемент дерева, если новый элемент включен в таблицу.
struct Node{
int key;
Node *left, *right;
};
Node *insert(Node **proot, int k)
{
Node **ptr = proot;
Node *cur;
/* поиск позиции в дереве для включения нового элемента;
можно использовать рассмотренную выше функцию find() */
while(*ptr){
if((*ptr)->key == k)
return NULL; /* элемент с таким ключом в таблице есть */
ptr = k < (*ptr)->key? &(*ptr)->left: &(*ptr)->right;
}
/* создание нового элемента дерева */
Node *cur = new Node;
if(!cur)
return NULL; /* нет свободной памяти */
cur->key = k;
cur->left = cur->right = NULL;
/* нашли позицию; включаем новый элемент */
*ptr = cur;
return cur;
}
Вариант (b), в силу рекурсивности дерева, можно рассматривать следующим образом. Если дерево пусто, новый элемент становится его корнем. Если дерево не пусто, в зависимости от соотношения ключей выбирается левое или правое поддерево, которое является деревом; для него вновь вызывается функция включения.
Для рекурсивной функции создание элемента дерева должно быть выполнено вне функции, поэтому удобно использовать две функции: основная функция включения нового элемента в дерево (insert()), которая создает новый элемент и вызывает функцию включения элемента в дерево, и рекурсивная функция включения в дерево (instree()). Тексты соответствующих функций приведены ниже.
struct Node{
int key;
Node *left, *right;
};
/* рекурсивная функция включения нового элемента в двоичное дерево.
* Результат – NULL, если элемент с таким ключом в таблице уже есть, или
* указатель на включенный элемент.
* Так как функция включает новый элемент в корень дерева (должно
* измениться значение указателя на корень дерева), в функцию нужно
* передать указатель на указатель на корень дерева – Node **.
*/
Node *instree (Node **proot, Node *newnode)
{
Node **ptr = proot;
if(!*proot){
/* дерево пусто */
*proot = newnode;
return newnode;
}
/* выбор нужного поддерева */
if((*proot)->key == newnode->key)
return NULL; /* элемент с таким ключом в таблице – дереве есть */
ptr = (newnode->key < (*proot)->key)?
&(*proot)->left: &(*proot)->right;
/* рекурсивный вызов функции включения нового элемента в выбранное
* поддерево */
return instree(ptr, newnode);
}
/* Функция включения нового элемента в таблицу. Результат – NULL, если
* элемент не может быть включен в таблицу, и указатель на новый элемент
* в противном случае
*/
Node *insert(Node **proot, int k)
{
Node *cur, *ptr;
/* создание нового элемента таблицы – дерева */
Node *cur = new Node;
if(!cur)
return NULL; /* нет свободной памяти */
cur->key = k;
cur->left = cur->right = NULL;
/* включение нового элемента в дерево */
if(!(ptr = instree(proot, cur)))
free(cur);
return ptr;
}
Тексты всех рассмотренных функций приведены также в файлах Programs/tab2bin.cpp и Programs/bintree.cpp.
С операцией удаления связаны определенные проблемы.
Удаление листа выполняется просто. Для этого достаточно в поле, содержащее ссылку на удаляемый элемент, записать значение пустой ссылки (рис. II-47).
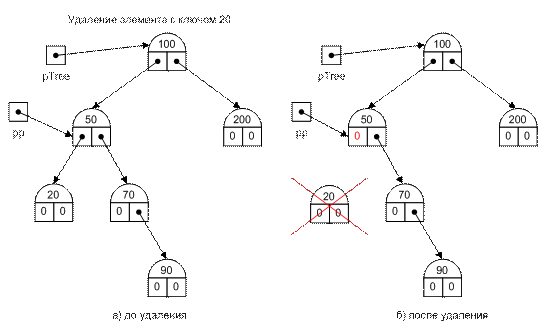
Рис. II-47.
При удалении промежуточной вершины необходимо сохранить упорядоченность вершин дерева. При этом потребуется определенная реорганизация дерева. Рассмотрим разные варианты, которые могут возникнуть при удалении промежуточной вершины дерева.
Вариант 1. Удаляемая вершина дерева имеет только одно подчиненное (левое или правое) поддерево. В этом случае в поле, содержащее ссылку на удаляемый элемент, следует записать значение ссылки на поддерево, подчиненное удаляемому элементу. Пусть, например, удаляется элемент с ключом 70. Он имеет подчиненное правое поддерево. Значения ключей в правом поддереве больше 70, но меньше 100. Поэтому запись в поле левой ссылки элемента с ключом 50 значения правой ссылки удаляемого элемента не нарушает упорядоченности вершин дерева (рис. II-48).
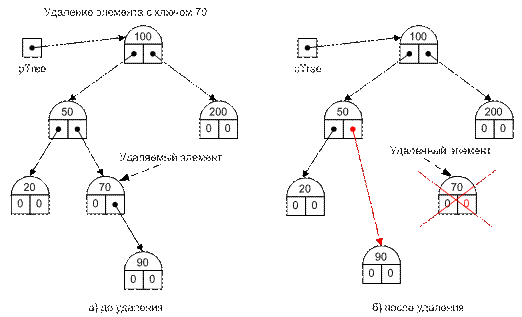
Рис. II-48.
Вариант 2. Удаляемая вершина имеет два поддерева. В этом случае она должна быть заменена каким-то существующим элементом дерева так, чтобы такая замена не потребовала дополнительной реорганизации дерева. Например, удаляемая вершина может быть заменена элементом с минимальным значением ключа из правого поддерева, подчиненного удаляемой вершине, или элементом с максимальным значением ключа из левого поддерева, подчиненного удаляемой вершине. Оба этих варианта равноправны.
В качестве элемента замены, для определенности, используем элемент с минимальным значением ключа из правого поддерева, подчиненного удаляемой вершине.
Элемент замены может быть непосредственно подчинен удаляемому элементу; в этом случае в поле левой ссылки элемента замены записывается значение ссылки на левое поддерево удаляемого элемента, а в поле, содержащее ссылку на удаляемый элемент, записывается ссылка на правое поддерево удаляемого элемента (рис II-49).
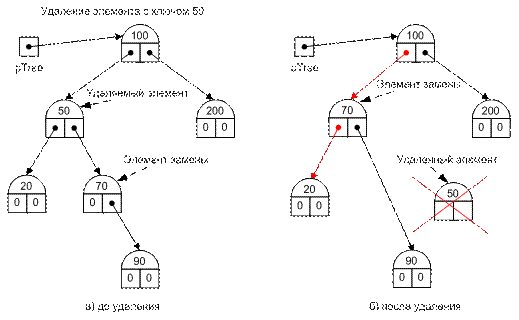
Рис. II-49.
Вариант 3. Удаляемая вершина имеет два поддерева, и элемент замены отстоит от удаляемого элемента более чем на один уровень. В этом случае, помимо тех операций, которые указаны в варианте 2, выполняются еще следующие. В поле левой ссылки элемента, ссылающегося на элемент замены, записывается значение ссылки на правое поддерево элемента замены, а в поле правой ссылки элемента замены записывается значение ссылки на правое поддерево удаляемого элемента (рис. II-50).
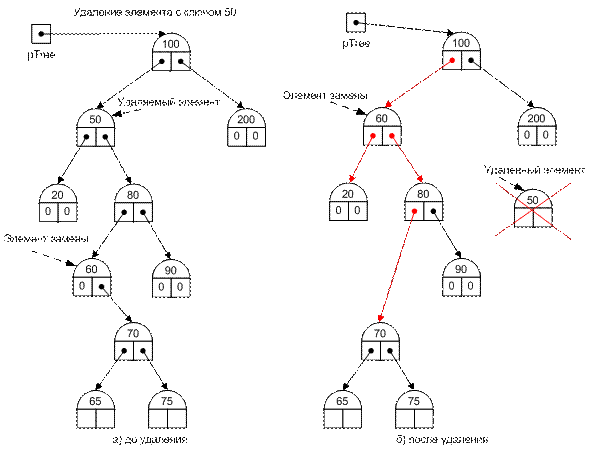
Рис. II-50.
Текст функции удаления приведен ниже и в файле Programs/bintree.cpp. В приведенном примере дерево определяется как внешний объект.
struct Node{
int key;
Node *left, *right;
};
Node *pTree;
int Del(int k)
{
// найти удаляемый элемент
Node **pp = Find(k);
if(!(*pp)) // поиск не успешен
return -1;
// Удаляемый элемент найден
Node *pd = *pp;
// Вариант 1. Удаляемый элемент имеет максимум одно поддерево (или является листом)
// В этом случае в родительскую вершину записывается его поддерево (или NULL)
if(pd->left == NULL)
*pp = pd->right;
else if(pd->right == NULL)
*pp = pd->left;
else{
// удаляемый элемент имеет два поддерева
// ищем самый маленький элемент в правом поддереве - т.е. элемент,
// у которого левая ссылка - NULL
Node **pch = &(*pp)->right;
while((*pch)->left)
pch = &(*pch)->left;
Node *pc = *pch;
// выполняем замещение элемента
// Вариант 2. Элемент с минимальным ключом из правого поддерева
// подчинен удаляемому элементу
*pp = pc;
pc->left = pd->left;
// Случай 3. Элемент с минимальным ключом из правого поддерева
// расположен ниже удаляемого на несколько уровней
if(pd->right!= pc){
// реорганизация фрагмента дерева с найденным для замены элементом
*pch = pc->right;
// вставляем элемент замены вместо удаляемого элемента
pc->right = pd->right;
}
}
// Освобождаем память
delete pd;
return 0;
}
 2015-08-12
2015-08-12 1026
1026