Пусть в пространстве 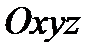 имеется некоторая область
имеется некоторая область 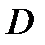 , в которой задана функция
, в которой задана функция 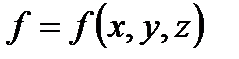 . В этом случае говорят, что в области
. В этом случае говорят, что в области 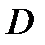 задано скалярное поле, а функцию
задано скалярное поле, а функцию 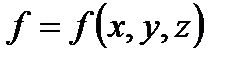 называют функцией поля.
называют функцией поля.
Подставим 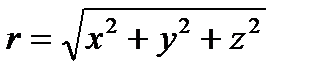 и
и 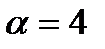 в функцию поля, которая дана в нашем примере:
в функцию поля, которая дана в нашем примере:
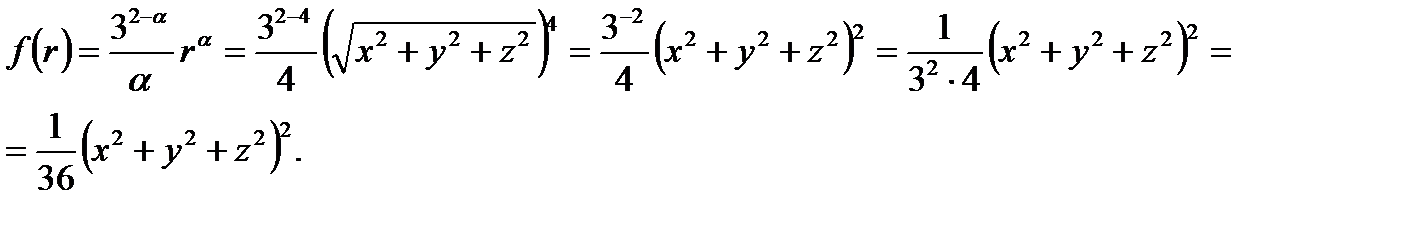
Мы записали функцию поля в виде 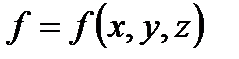 .
.
Градиентом скалярного поля, заданного дифференцируемой функцией 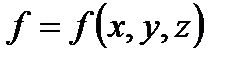 , называется вектор, координаты которого совпадают со значениями соответствующих частных производных этой функции:
, называется вектор, координаты которого совпадают со значениями соответствующих частных производных этой функции:
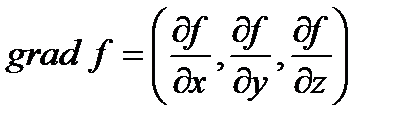 , или
, или 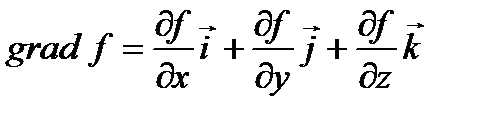 .
.
Частная производная функции нескольких переменных – это производная функции одной переменной, когда значение остальных переменных фиксировано.
Чтобы найти градиент в нашем примере, вычислим частные производные функции поля:
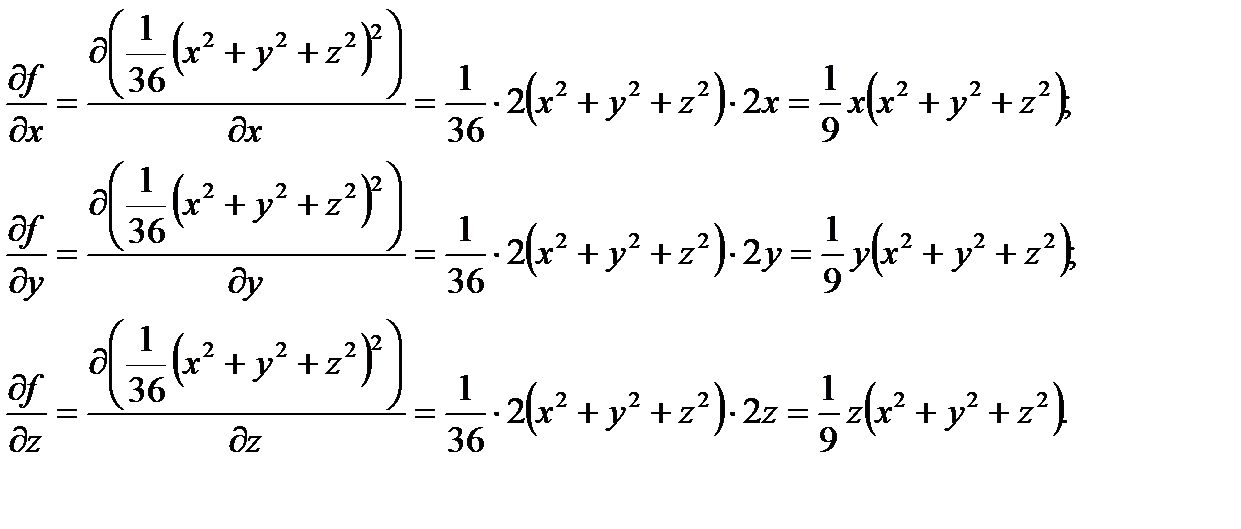
Поэтому градиент скалярного поля равен:
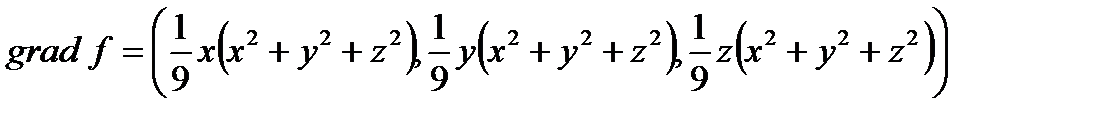
или
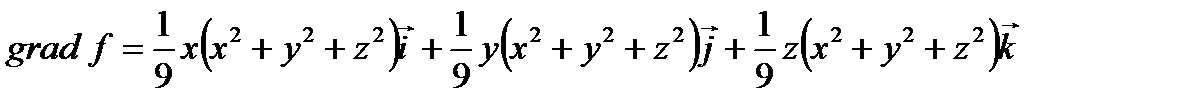
Производной функции 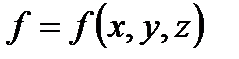 в точке
в точке 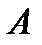 по направлению
по направлению 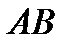 (обозначают
(обозначают 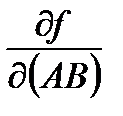 ) называется предел отношения приращения функции в направлении
) называется предел отношения приращения функции в направлении 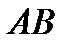 к величине приращения
к величине приращения 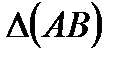 при
при 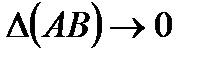 :
:
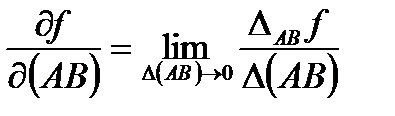 .
.
Формула для вычисления производной по направлению:
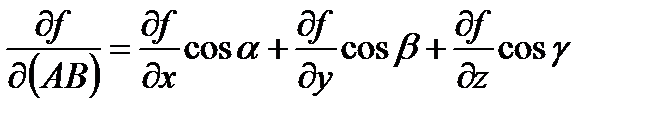 , где
, где 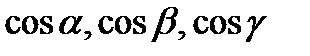 – направляющие косинусы (косинусы углов, которые вектор образует с положительными полуосями координат). Для вектора с координатами
– направляющие косинусы (косинусы углов, которые вектор образует с положительными полуосями координат). Для вектора с координатами 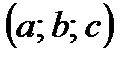 направляющие косинусы равны:
направляющие косинусы равны: 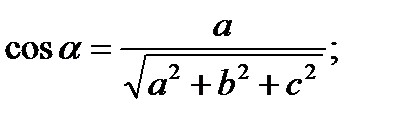
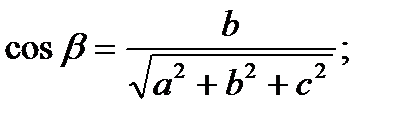
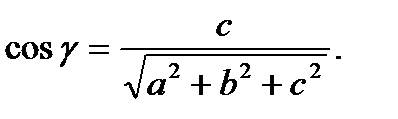
Вектор 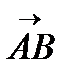 , по направлению которого требуется найти производную скалярного поля, задан координатами начала и конца. Чтобы найти координаты этого вектора, из координат конца вычтем координаты начала. Соответствующие разности будут координатами вектора
, по направлению которого требуется найти производную скалярного поля, задан координатами начала и конца. Чтобы найти координаты этого вектора, из координат конца вычтем координаты начала. Соответствующие разности будут координатами вектора 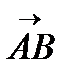 :
:
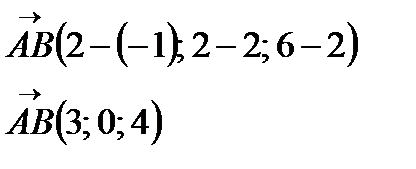
или
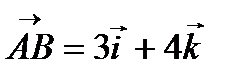
Найдём значения частных производных в точке 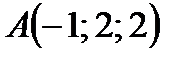 :
:
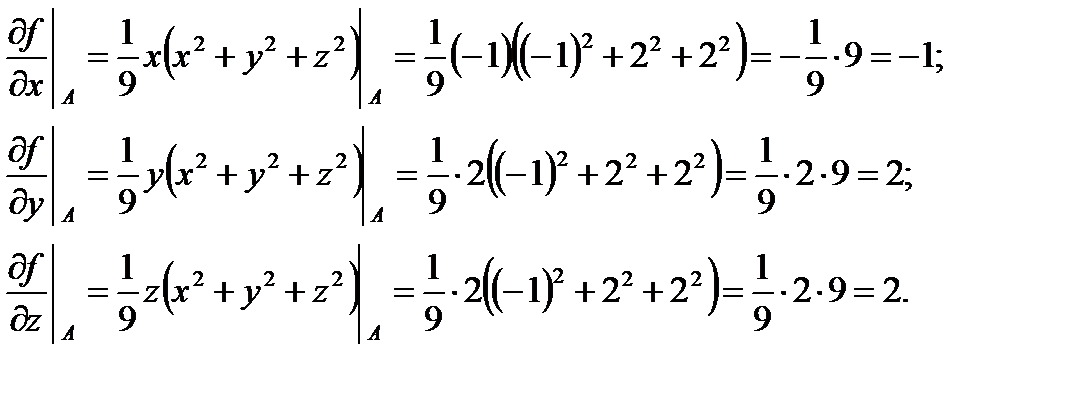
Найдём длину вектора 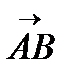 :
: 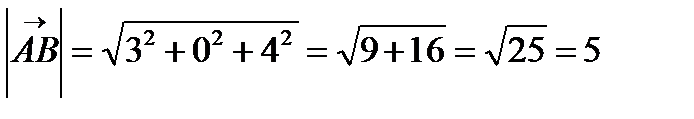 , тогда
, тогда 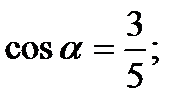
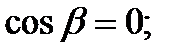
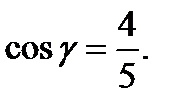
Подставим значения частных производных и направляющих косинусов в формулу для нахождения производной по направлению:
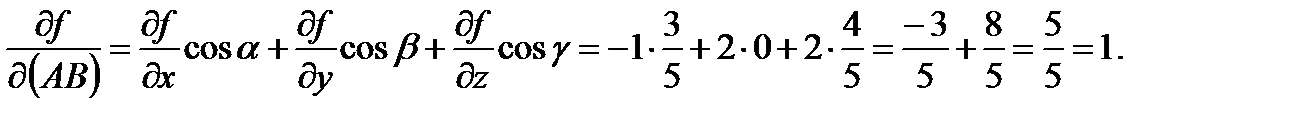
Ответ:
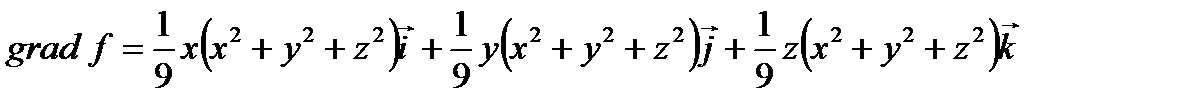 ;
;
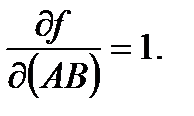
 2015-08-13
2015-08-13 225
225






