Озвучивается тема урока.
Вопрос: Какое свойство позволило нам привести дроби к новому знаменателю?
Ответ: Основное свойство дроби.
Мы можем умножать числитель и знаменатель дроби на одно и то же натуральное число.  =
= 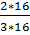 =
= 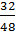 ;
;  =
= 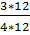 =
= 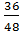 .
.
Вопрос (проблема): А как привести дробь 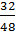 к знаменателю 3,4, 6, 8, 12, 16, 24?
к знаменателю 3,4, 6, 8, 12, 16, 24?
Ответ: Делить (на 16, 12, 8, 6, 3, 4, 2).
Основное свойство дроби позволяет нам делить числитель и знаменатель на одно и то же натуральное число. 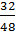 =
= 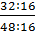 =
=  ;
; 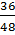 =
=  =
= 
Числитель и знаменатель дроби 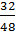 делили на наибольший общий делитель чисел 32 и 48. Это число 16.
делили на наибольший общий делитель чисел 32 и 48. Это число 16.
Числитель и знаменатель дроби 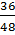 делили на наибольший общий делитель чисел 36 и 48. Это число 12.
делили на наибольший общий делитель чисел 36 и 48. Это число 12.
Числитель и знаменатель дробей 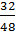 и
и 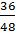 можно делить на общий делитель числителя и знаменателя: на 2, на 4.
можно делить на общий делитель числителя и знаменателя: на 2, на 4. 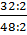 =
= 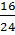 ;
; 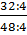 =
= 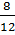 ;
;  =
= 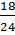 ;
;  =
= 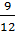
Определение. Деление числителя и знаменателя дроби на их общий делитель, отличный от единицы, называют сокращением дроби.
Вопрос: Можно ли сократить дробь 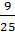 ?
?
Ответ: Нет. У этих чисел нет общего делителя.
Дроби 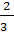 и
и  тоже нельзя разделить на общий делитель числителя и знаменателя, а значит сократить нельзя. Числа 25 и 9, 2 и 3, а также 3 и 4 взаимно простые.
тоже нельзя разделить на общий делитель числителя и знаменателя, а значит сократить нельзя. Числа 25 и 9, 2 и 3, а также 3 и 4 взаимно простые.
Определение. Дробь, числитель и знаменатель которой взаимно простые числа, называется несократимой. Приведите свои примеры.
Рассмотрим способы сокращения дробей.
1. Сокращать дроби можно постепенно, используя признаки делимости.
Например: 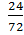 =
= 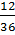 =
= 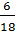 =
=  =
= 
2. Найти НОД числителя и знаменателя. Разделить числитель и знаменатель дроби на их наибольший общий делитель.
Например: НОД(24,72)=24. 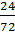 =
=  =
= 
3. Разложить числитель и знаменатель дроби на простые множители. Сократить дробь на произведение общих множителей.
Например: 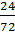 =
= 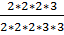 =
= 
 2015-08-13
2015-08-13 534
534








