Правила нахождения производных

26. Задание {{ 26}} {712354363}-2.2-1 Тема 2-2-0

Дана функция 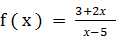. Производная этой функции в точке х = - 1

(т. е. 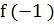) имеет значение…..

-#: f ' (-1) =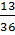

+#: f ' (- 1) = –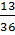

-#: f ' (- 1) =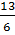

-#: f ' (- 1) = -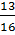

27. Задание {{ 27 }} {712354363}-2.2-2 Тема 2-2-0

Производная функции у = х² ∙ 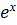имеет вид…..

-#: у ^' = 2х ∙ 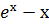²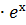

+#: у ^' = 2х ∙ ∙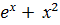

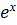
-#: у ^'= 2х +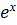

-#: у ^' = 2х ∙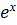

28. Задание {{ 28 }} {712354363}-2.2-3 Тема 2-2-0

Производная функции у = х ∙ 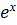имеет вид…..

-#: у^'= х ∙

+#: у ^' = х ∙ ∙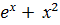

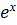
-#: у^'= 2х +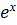

-#: у ^' =х ∙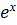

29. Задание {{ 29 }} {712354363}-2.2-4 Тема 2-2-0

Используя формулы дифференцирования, найдите производную функции f(x)=x³ в точке x₀=-1

-#: -3

+#: 3

-#: 2

-#: 1

30. Задание {{ 30 }} {712354363}-2.2-5 Тема 2-2-0

Используя формулы дифференцирования, найдите производную функции f(x)=x⁵в точке x₀=-1

-#: -5

+#: 5

-#: 2

-#: 1

Производная сложной функции.

31. Задание {{ 31}} {712354363}-2.3-1 Тема 2-3-0

Производная функции у = 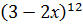имеет вид…..

-#: у^'=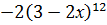

+#: у^'= - 24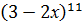

-#: у ^' = 24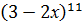

-#: иной ответ

32. Задание {{ 32}} {712354363}-2.3-2 Тема 2-3-0

Производная функции у = 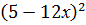имеет вид…..

-#: у ^' =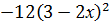

+#: у ^'= 144х-60

-#: у ^' = - 144х +60

-#: иной ответ