Первый подход связан с использованием метода регуляризации, предложенного
в 1963 г. российским математиком А. Н. Тихоновым [50]. Суть этого метода заключается в том, чтобы видоизменить функционал качества таким образом, чтобы он всегда имел минимум и положение этого минимума непрерывно зависело от параметра регуляризации.
Модификация функционала качества. Типичный функционал качества, который используется при обучении нейронных сетей с прямой передачей, – это функционал средней суммы квадратов ошибки обучения
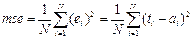 . (3.33)
. (3.33)
Если модифицировать функционал добавлением слагаемого вида
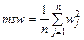 , (3.34)
, (3.34)
то это будет означать, что большие значения настраиваемых параметров при обучении сети будут существенно штрафоваться, а это вынудит реакцию сети быть более гладкой и снизит вероятность возникновения явления переобучения.
Введем параметр регуляризации g и построим следующий регуляризирующий функционал:
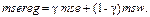 (3.35)
(3.35)
Рассмотрим нейронную сеть типа 1–5–1 с одним входом, пятью скрытыми нейронами и одним выходом. Эта сеть использует те же типы нейронов, что и предыдущая сеть, но количество скрытых нейронов в 6 раз меньше, предельное количество циклов обучения сокращено до 100, а параметр регуляризации равен 0.9998.
net = newff([–1 1],[5,1],{'tansig','purelin'},'trainbfg');
net.trainParam.epochs = 100;
net.trainParam.show = 50;
net.trainParam.goal = 1e–5;
net.performFcn = 'msereg';
net.performParam.ratio = 0.9998;
p = [–1:0.05:1];
t = sin(2*pi*p)+0.1*randn(size(p)); % Возмущенные значения функции
t1 = sin(2*pi*p); % Обучающая последовательность
[net,tr] = train(net,p,t); % Рис.3.21,а
an = sim(net,p); % Значения аппроксимирующей функции
plot(p,t,'+',p,an,'–',p,t1,':') % Рис.3.21,б
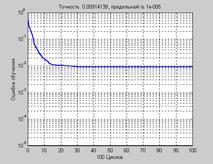
На рис. 3.21, а показан график изменения ошибки обучения, из которого следует, что ошибка обучения составляет величину порядка 0.01; на рис. 3.21, б показаны результаты аппроксимации, из которых следует, что при использовании пяти нейронов в скрытом слое переобучение не наблюдается, кривая выхода аппроксимирует функцию синуса,
но точность аппроксимации недостаточна.
 а а | 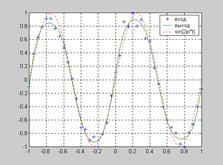 б б |
Рис. 3.21
Сложность применения метода регуляризации состоит в том, что очень трудно определить оптимальное значение параметра регуляризации и количество требуемых нейронов. Ниже представлен алгоритм, который позволяет автоматически установить параметр регуляризации.
Автоматическая регуляризация. Автоматический выбор параметра регуляризации может быть реализован на основе правила Байеса. Этот подход был предложен Д. Мак-Кейем (D. MacKay) [27] и состоит в том, что веса и смещения сети рассматриваются как случайные величины с известным законом распределения. Параметр регуляризации связан с дисперсией этого распределения и может быть оценен с использованием статистических методов. Детальное описание процедуры регуляризации с использованием правила Байеса и алгоритма Левенберга – Марквардта можно найти в работе [11]. Соответствующая процедура реализована в виде М-функции trainbr.
Вновь обратимся к нейронной сети типа 1–20–1, предназначенной для решения задачи аппроксимации функции синуса.
net = newff([–1 1],[20,1],{'tansig','purelin'},'trainbr');
Функция trainbr характеризуется следующими параметрами, заданными по умолчанию:
net.trainParam
ans =
epochs: 100
show: 25
goal: 0
time: Inf
min_grad: 1e–010
max_fail: 5
mem_reduc: 1
mu: 0.005
mu_dec: 0.1
mu_inc: 10
mu_max: 1e+010
Этот список соответствует списку параметров М-функции trainlm.
Установим следующие значения этих параметров:
net = newff([–1 1],[20,1],{'tansig','purelin'},'trainbr');
net.trainParam.epochs = 50;
net.trainParam.show = 10;
randn('seed',192736547);
p = [–1:.05:1];
t = sin(2*pi*p)+0.1*randn(size(p));
net = init(net);
net = train(net,p,t); % Рис.3.22
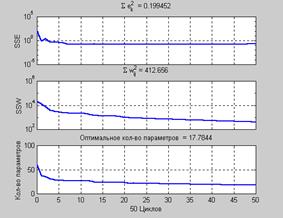 Рис. 3.22
Рис. 3.22
На рис. 3.22 показаны изменения суммы квадратов ошибок и весов, а также оптимальное количество настраиваемых параметров нейронной сети. В данном случае после обучения используется приблизительно 18 – из общего числа 61 – параметров сети типа 1–20–1.
Построим графики исследуемых функций:
an = sim(net,p); % Значения аппроксимирующей функции
t1 = sin(2*pi*p); % Значения аппроксимируемой функции
plot(p,t,'+',p,an,'–',p,t1,':') % Рис. 3.23
Рис. 3.23 иллюстрирует реакцию построенной нейронной сети при решении задачи аппроксимации. В отличие от рис. 3.19, на котором видно, что в сети существует переобучение, здесь мы видим, что реакция сети близка к основной функции синуса. Следовательно, сеть хорошо приспособлена к новым входам. Можно попробовать реализовать более мощную исходную сеть, но при этом в реакции сети никогда не будет проявляться эффект переобучения. Таким образом, процедура обучения trainbr представляет собой некоторую регулярную процедуру для определения оптимального числа настраиваемых параметров и, как следствие, оптимального размера сети.
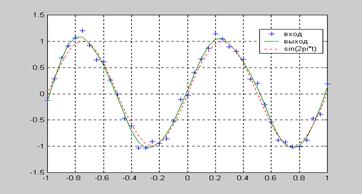 Рис. 3.23
Рис. 3.23
 2015-08-21
2015-08-21 1532
1532








