Для решения задач линейного программирования предложено немало различных алгоритмов. Наиболее эффективным среди них является алгоритм, известный под названием симплекс-метод или метод последовательного улучшения плана. Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949 г., однако идея этого метода была разработана российским математиком в 1939 г. Канторовичем Леонидом Витальевичем. Симплексный метод – это итерационный процесс, который начинается с одного решения и в поисках лучшего варианта движется по угловым точкам области возможных решений до тех пор, пока не достигнет оптимального значения. Симплексный метод базируется на введении дополнительных переменных, так называемых, базисных, которые позволяют образовать единичную матрицу, в которой не допускаются отрицательные и другие числа, кроме нуля и единицы. Наличие единичной матрицы является необходимым условием при решении задач симплекс-методом.
1. Для того чтобы решить ЗЛП симплекс-методом, необходимо систему ограничений и линейную форму (1)-(3) представить в каноническом виде (4). Этот вид характеризуется следующими особенностями.
А) Система ограничений имеет только форму уравнений, в уравнениях выделены базисные неизвестные. Базисные неизвестные – это неизвестные, которые были добавлены при переходе от неравенств к равенствам. Коэффициенты при базисных неизвестных в системе ограничений образуют единичную матрицу.
Б) Линейная форма F,которую требуется максимизировать, должна быть выражена только через свободные неизвестные и вместе с ними записана в левой части уравнения.
В) Все неизвестные 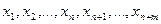 должны быть неотрицательны, и все свободные члены
должны быть неотрицательны, и все свободные члены 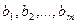 должны быть неотрицательны. Условие
должны быть неотрицательны. Условие 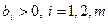 может быть обеспечено только в том случае, когда система ограничений в задаче ЛП имеет хотя бы одно неотрицательное решение.
может быть обеспечено только в том случае, когда система ограничений в задаче ЛП имеет хотя бы одно неотрицательное решение.
Базисным неизвестным 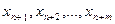 системы ограничений в каноническом виде соответствует неотрицательное базисное решение
системы ограничений в каноническом виде соответствует неотрицательное базисное решение 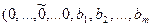 ). Это решение еще называют опорным планом. Это решение получается из системы ограничений в виде уравнений (4), если в ней свободные неизвестные
). Это решение еще называют опорным планом. Это решение получается из системы ограничений в виде уравнений (4), если в ней свободные неизвестные 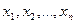 приравнять к нулю. При этом форма F примет значение со. Симплекс-метод состоит в переходе от одного базисного решения системы уравнений к другому базисному решению, такому, что значение формы Fпри этом увеличивается (не уменьшается). При этом существенно используется условие неотрицательности неизвестных.
приравнять к нулю. При этом форма F примет значение со. Симплекс-метод состоит в переходе от одного базисного решения системы уравнений к другому базисному решению, такому, что значение формы Fпри этом увеличивается (не уменьшается). При этом существенно используется условие неотрицательности неизвестных.
2. Составляется табл. 1.
3. Просматриваются элементы последней строки табл. 1 (элемент с0 (см. табл. 1) в рассмотрение не принимается).
· Если среди них нет отрицательных, то базисное решение, соответствующее табл. 1, является оптимальным и 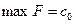 . В базисном решении свободные неизвестные равны нулю, а базисные принимают значения свободных членов.
. В базисном решении свободные неизвестные равны нулю, а базисные принимают значения свободных членов.
· Если в последней строке симплексной таблицы оптимального плана находится нуль, принадлежащий свободной переменной, не вошедшей в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов. Свободную переменную, соответствующую указанному столбцу, можно внести в базис, выполнив соответствующие этапы алгоритма. В результате будет получен второй оптимальный план с другим набором базисных переменных.
4. Выбор разрешающего столбца. Если в последней строке найдется хотя бы один отрицательный элемент, например с j < 0, то, отметив j -й столбец стрелкой ↓ в верхней части табл. 1, переходят к пункту 5. Если нет отрицательных элементов, то оптимальное решение найдено.
5. Просматривают элементы 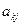 разрешающего выделенного столбца над элементом с j<0. Если среди них нет положительных, то
разрешающего выделенного столбца над элементом с j<0. Если среди них нет положительных, то 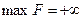 .
.
6. Если найдется хотя бы один положительный элемент, то для положительных элементов отмеченного столбца вычисляют отношения 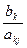 , где
, где 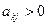 и b k – свободный член из строки, соответствующей рассматриваемому положительному элементу отмеченного разрешающего столбца. Вычисленные отношения заносят в последний столбец табл. 1.
и b k – свободный член из строки, соответствующей рассматриваемому положительному элементу отмеченного разрешающего столбца. Вычисленные отношения заносят в последний столбец табл. 1.
7. Выбор разрешающей строки. Выбирают наименьшее из этих отношений. Пусть оно достигается при k = i. Отмечают i -ю строку стрелкой → в левой части табл. 1. Строку называют разрешающей. Объявляют элемент a ij, стоящий на пересечении выделенных строки и столбца разрешающим (ведущим). Он обведен рамкой в табл. 1.
8. Составляют табл. 2. В базис (см. 1-й столбец табл. 2) на место базисного неизвестного x i ставят свободное неизвестное x j. Делят элементы отмеченной строки табл. 1 на разрешающий элемент a ij и вносят полученные элементы в ту же i -ю строку табл. 2. Умножая строку табл. 1 на соответствующие числа, прибавляют ее к строкам табл. 1, см. метод Гаусса, с тем, чтобы получить выше и ниже разрешающего a ij элемента нули. Все вновь вычисленные элементы строк вносят в табл. 2. Можно пересчитывать элементы для новой таблицы 2 по правилу прямоугольника:
Для этого выбирают из старого плана (табл. 1) четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. Во второй вершине на одной диагонали с разрешающим элементом находится старое значение элемента, которое указывает на место расположения нового элемента НЭ в новом плане II (табл. 2). Третий элемент А и четвертый элемент В завершают построение прямоугольника в недостающих двух вершинах и расположены по другой диагонали. Значение нового элемента в плане II находится из выражения: НЭ= СЭ – (А*В) / РЭ. Все элементы, расположенные на пересечении строк и столбцов, соответствующих одноименным новым базисным элементам, равны 1, остальные элементы столбца в новых базисах векторов, включая индексную (последнюю) строку, равны 0. Аналогично проводятся расчеты по всем строкам таблицы, включая индексную (последнюю строку таблицы) строку. Выполняя последовательно все этапы алгоритма, формируем план II.
9. С таблицей 2 обращаются к пункту 3.
Исходная математическая модель ЗЛП имеет вид:
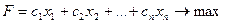 (1)
(1)
при следующих ограничениях на переменные:
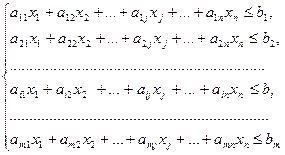 (2)
(2)
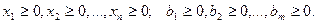 (3)
(3)
Каноническая форма ЗЛП имеет такой вид:
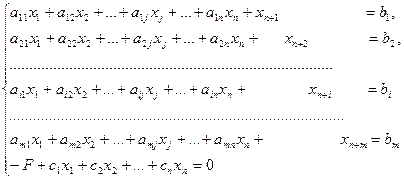 (4)
(4)
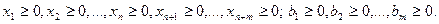
 Табл. 1
Табл. 1
| Базис | Своб. члены | x1 | … | 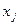
| … | xn | xn+1 | … | 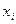
| … | xn+m | 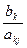
|
| xn+1 | b1 | a11 | … | a1j | … | a1n | … | … | ||||
| xn+2 | b2 | a21 | … | a2j | … | a2n | … | … | ||||
| … | … | … | … | … | … | … | … | … | … | … | … | |
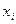 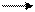
| bi | ai1 | … | aij | … | ain | … | … | ||||
| … | … | … | … | … | … | … | … | … | … | … | … | |
| xn+m | bn+m | am1 | … | amj | … | amn | … | … | ||||
| F | c0 | c1 | … | cj | … | cn | … | … |
Табл. 2
| Базис | Своб. члены | x1 | … | 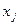
| … | xn | xn+1 | … | 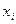
| … | xn+m | 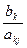
|
| xn+1 | b'1 | a'11 | … | … | a'1n | … | … | |||||
| xn+2 | b'2 | a'21 | … | … | a'2n | … | … | |||||
| … | … | … | … | … | … | … | … | … | … | … | … | |
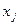
| 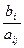
| 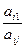
| … | … | 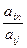
| … | 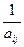
| … | ||||
| … | … | … | … | … | … | … | … | … | … | … | … | |
| xn+m | b'n+m | a'm1 | … | … | a'mn | … | … | |||||
| F | c'0 | c'1 | … | … | c'n | … | … |
 2015-08-21
2015-08-21 650
650






