Регулярные языки и конечные автоматы

Лабораторная работа №3

Разработка лексического анализатора выполняется достаточно просто, если используется теория регулярных языков и конечных автоматов. Рамках этой теории классы однотипных лексем рассматриваются как формальные языки (язык идентификаторов, язык констант и т.д.), множество предложений которых описывается с помощью соответствующей порождающей грамматики. При этом языки эти настолько просты, что они порождаются простейшей из грамматик – регулярной грамматикой.

Определение 1. порождающая грамматика G = <N, T, P, S>, правила которой имеют вид: А::=аВ или С::=b, где А, В,С Є N; a, b Є Т называется регулярной (автоматной).

Язык L (G), порождаемый автоматной грамматикой, называется автоматным (регулярным) языком или языком с конечным числом состояний.

Пример 1. Класс идентификаторов, если идентификатором является последовательность, состоящая из букв и цифр, и первым символом идентификатора может быть только буква, описывается следующей порождающей регулярной грамматикой G = <N, T, P, S>, в которой

N= {I, K}, T = {б, ц}, S={I},

P = { 1. I::= б

2. I::= бК

3. К::= бК

4. К::= цК

5. К::= б

6. К::= ц }

Здесь б, ц – обобщенные терминальные символы для обозначения букв и цифр соответственно.

Процесс порождения идентификатора «ббцбц» описывается следующей последовательностью подстановок

I => бК => ббК => ббцК => ббцбК => ббцбц

Однако основной задачей ЛА является не порождение лексических единиц, а их распознавание. Математической моделью процесса распознавания регулярного языка является вычислительное устройство, которое называется конечным автоматом (КА). Термин «конечный» подчеркивает то, что вычислительное устройство имеет фиксированный и конечный объем памяти и обрабатывает последовательность входных символов, принадлежащих некоторому конечному множеству. Существуют различные типы КА, если функцией выхода КА (результатом работы) является лишь указание на то, допустима или нет входная последовательность символов, такой КА называют конечным распознавателем.

Определение 2. Конечным автоматом называется следующая пятерка:

А = <V, Q, δ, q₀, F>, где V = {a₁, a₂, …, a_m} – входной алфавит (конечное множество символов);

Q = {q₀, q₁, …, q_n-1} – алфавит состояний (конечное множество символов);

δ: Q ×V →Q – функция переходов;

q₀ Є Q – начальное состояние конечного автомата;

F Є Q – множество заключительных состояний.

Схема функционирования КА.

Имеется бесконечная лента, разбитая на ячейки, в каждой из которых может находиться один символ из V. На ленте записана цепочка α Є V*. Ячейки слева и справа от цепочки не заполнены. Имеется конечное устройство управления (УУ) с читающей головкой, которое может последовательно считывать символы с ленты, передвигаясь вдоль ленты слева направо. При этом, УУ может находиться в каком – либо одном состоянии из Q. Начинает свою работу УУ всегда в начальном состоянии q₀, а завершает в одном из заключительных состояний F. Каждый раз, переходя к новой ячейке на ленте, УУ переходит в новое состояние в соответствии с функцией δ.

Функцию переходов КА можно представить следующими способами:

· Совокупность команд;

· Диаграмма состояний;

· Таблица переходов.

Команда конечного автомата записывается следующим образом:

(q_i, a_j) → q_k, где q_i, q_k Є Q; a_j Є V.

Данная команда обозначает, что конечный автомат находится в состоянии q_i, читает с ленты символ а_j и переходит в состояние q_k.

Графически команда представляется в виде дуги графа, идущей из вершины q_i в вершину q_k и помеченной символом a_j входного алфавита:

Графическое представление всего отображения δ называют диаграммой состояний конечного автомата.

Если КА оказывается в ситуации (q_i, a_j), которая не является левой частью какой – либо команды, то он останавливается. Если же УУ считает все символы цепочки α, записанной на ленте, и при этом перейдет в заключительное состояние q_r Є F, то говорят, что цепочка α допускается конечным автоматом.

Таблица переходов КА строится следующим образом: столбцы матрицы соответствуют символам из входного алфавита, строки – символам из алфавита состояний, а элементы матрицы соответствуют состояниям, в которые переходит КА для данной комбинации входного символа и символа состояния.

Пусть задана регулярная грамматика G = <N, T, P, S>, правила которой имеют вид: А_i::= a_jA_k или А_i::= a_j, где А_i, A_k Є N и a_j Є Т.

Тогда конечный автомат А = <V, Q, δ, q₀, F>, допускающий тот же самый язык, что порождает регулярная грамматика G, строится следующим образом:

1) V = T;

2) Q = N U {Z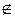}, Z N и Z 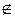T, Z – заключительное состояние КА;

3) q₀ = {S};

4) F = {Z};

5) Отображение δ строится в виде:

· Каждому правилу подстановки в грамматике G вида А_i::= a_jA_k ставится в соответствие команда (А_i, a_j) → A_k;

· Каждому правилу подстановки вида А_i::= a_j ставится в соответствие команда (А_i, a_j) → Z;

Пример 2. Построить КА для грамматики из примера 1. Имеем А = <V, Q, δ, q₀, F>, где

1) V = T = {б, ц}

2) Q = N U {Z} = {I, R, Z}

3) q₀ = {S} = {I}

4) F = {Z}

5) δ: a) в виде совокупности команд:

(I, б) → Z

(I, б) → K

(K, б) → K

(K, ц) → K

(K, б) → Z

(K, ц) → Z

б) в виде диаграммы состояний

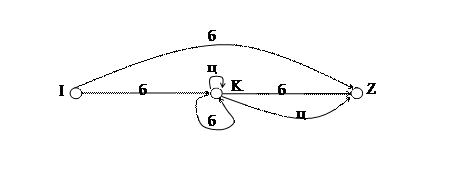
Различают детерминированные и недетерминированные конечные автоматы. КА называется недетерминированным КА (НКА), если в диаграмме его состояний из одной вершины исходит несколько дуг с одинаковыми пометками. Например, КА из примера 2 является НКА.

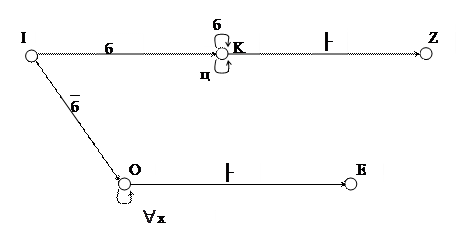
Для практических целей необходимо, чтобы конечный распознаватель сам определял момент окончания входной последовательности символов с выдачей сообщения о правильности или ошибочности входной цепочки. Для этих целей входная цепочка считается ограниченной справа концевым маркером ├ и в диаграмму состояний КА вводятся интерпретированные состояния:

Z – «допустить входную цепочку»;

О – «запомнена ошибка во входной цепочке»;

Е – «отвергнуть входную цепочку».

Состояния Z и Е являются заключительными, и в них КА переходит при прочтении концевого маркера ├ соответственно после обработки правильной или ошибочной входной цепочки. Состояние О является промежуточным, в него КА переходит из любого допустимого состояния КА при обнаружении ошибки во входной цепочке и остается в нем до поступления концевого маркера ├, после чего осуществляется переход в состояние Е – «отвергнуть входную цепочку».