Если число переменных в задаче линейного программирования больше двух, то ее решение графическим способом трудно выполнимо, так как требуется построение не на плоскости, а в пространстве. Для решения таких задач разработан специальный алгебраический симплекс-метод. Оптимальное решение будет находиться в одной из вершин многогранника допустимых решений. Продвигаясь по выпуклому многограннику ограничений от вершины к вершине, проверяется значение целевой функции и выбирается наилучшее.
Алгоритм симплекс-метода имеет следующий вид.
Шаг 1: Выберем m переменных, задающих допустимое пробное решение. Исключим эти переменные из выражения для целевой функции.
Шаг 2: Проверяем возможность улучшения значения целевой функции за счет одной переменной, приравненной вначале к нулю. Если это возможно, переходим к шагу 3. Иначе прекратим вычисления.
Шаг 3: Находим предельное значение переменной, за счет которой можно улучшить значение целевой функции. Увеличение значения этой переменной допустимо до тех пор, пока одна из m переменных, вошедших в пробное решение, не обратится в 0. Исключим из выражения для целевой функции эту переменную и введем в пробное решение ту переменную, за счет которой результат может быть улучшен.
Шаг 4: Решаем систему m уравнений относительно переменных, вошедших в новое пробное решение. Исключим эти переменные из выражения для целевой функции. Переходим к шагу 2.
Этот алгоритм приводит к оптимальному решению для любой модели линейного программирования за конечное число итераций (более подробно алгоритм представлен в прил. 1).
Пример
Фирма «Мультиконвейер» имеет возможность реализовать от одного до четырех различных типов технологических процессов. Технологические процессы первого и второго типов ориентированы на получение продукции А, а технологические процессы третьего и четвертого типов - на получение продукции B. Расходы, связанные с каждым из технологических процессов, приведены в табл. 1.
Таблица 1
| На единицу продукции А | На единицу продукции В | Имеется в наличии (всего) | |||
| техпроцесс 1 | техпроцесс 2 | техпроцесс 3 | техпроцесс 4 | ||
| Трудозатраты, человеко- - недель | ≤ 15 | ||||
| Количество материала Y, кг | ≤ 120 | ||||
| Количество материала Z, кг | ≤ 100 | ||||
| Доход с единицы продукции, усл.ед. |
Определить количество продукции, выпускаемой с помощью каждого технологического процесса, чтобы доход был максимален.
Решение
Составим математическую модель задачи.
Пусть Х1, Х2, Х3, Х4 – объем продукции, производимой с помощью соответственно 1, 2, 3, 4 технологических процессов.
Целевая функция имеет вид:
F (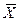 ) = 4X1 +5X2 +9Х3 +11Х4 → max,
) = 4X1 +5X2 +9Х3 +11Х4 → max,
Ограничения по материалу Y: 7X1 + 5X2 + 3Х3 +2Х4 ≤ 120;
ограничения по материалу Z: 3X1 + 5X2 + 10Х3 + 15Х4 ≤ 100;
ограничения по трудозатратам: 1X1 + 1X2 + 1Х3 +1Х4 ≤ 15;
Х1, Х2, Х3, Х4 ≥ 0.
Введем в рассмотрение свободные переменные Х5, Х6, Х7 и обозначим значение целевой функции через Х0. При этом задача линейного программирования примет нормальный вид.
В результате получим следующую систему уравнений:
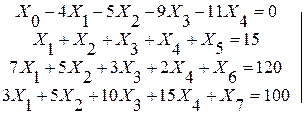 (1)
(1) 
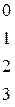
Нулевая строка – это преобразованная целевая функция.
Итерация 1
Выбираем пробное решение при Х0=0 и Х1, Х2, Х3, Х4 = 0:
Х5 =15;
Х6 = 120
Х7 = 100.
Такое решение называется исходным базисным решением, а переменные Х0, Х5, Х6, Х7 - базисными переменными, остальные переменные – небазисные.
Если под Х0 понимать прибыль, то из нулевой строки видно, что увеличение любого небазисного значения приводит к увеличению Х0, то есть прибыли. (Каждый коэффициент небазисных переменных в строке 0 определяет положительное приращение Х0, если перед ним стоит знак «-», или отрицательное приращение Х0, если перед ним стоит знак «+», при увеличении соответствующей небазисной переменной на 1.)
Шаг 2 устанавливает правило, позволяющее определить, какие переменные должны войти в следующий пробный базис.
Симплекс-критерий 1 (выбор разрешающего столбца). Если в нулевой строке все коэффициенты отрицательные, то следует выбрать наибольший по модулю коэффициент, так как именно он обеспечивает наибольшее удельное приращение значения целевой функции.
Такой переменной является Х4. Следовательно Х4 нужно включить в базис. Увеличение переменной Х 4 имеет ограничения, то есть её рост возможен лишь за счет уменьшения значений базисных переменных в каждой строке, содержащей Х4 с положительным коэффициентом. Так в строке 1 параметр Х5 должен быть меньше на 1, в строке 2 параметр Х6 должен быть меньше на 2, а в строке 3 параметр Х7 должен быть меньше на 15.
Симплекс-критерий 2 (выбор разрешающей строки). Рассматриваются отношения чисел, стоящих в правых частях уравнений (1) к соответствующим коэффициентам новой базисной переменной Хj и выбирается отношение с наименьшим значением. В очередном пробном решении Хj приравнивается именно к этому значению.
Рассмотрим отношения чисел, стоящих в правой части уравнений 1, 2, 3 к коэффициентам новой базисной переменной:
(1) 15/1,
(2) 120/2,
(3) 100/15.
Наименьшее значение соответствует третьему уравнению, следовательно оно будет разрешающим.
Коэффициент при Х4 в строке 3 сделаем равным 1, для чего разделим эту строку на 15:
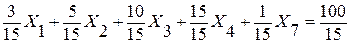 или
или
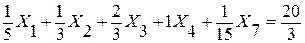 .
.
Данная процедура называется процедурой замены базиса.
В строках 0, 1, 2 коэффициент при Х4 должен быть равен 0. Для этого:
строку 3 умножаем на 11 и складываем со строкой 0, так как коэффициент при Х4 в строке 0 равен (-11)
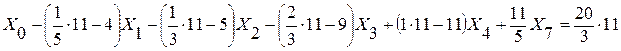 ,
,
то есть 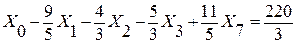 .
.
Аналогично строку 3 умножаем на (-1) и складываем со строкой 1, так как коэффициент при Х4 в строке 1 равен (+1);
строку 3 умножаем на (-2) и складываем со строкой 2, так как коэффициент при Х4 в строке 3 равен (+2).
После преобразований получаем систему уравнений:
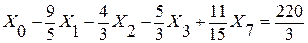 строка 0
строка 0
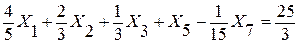 1
1
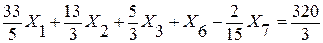 2
2
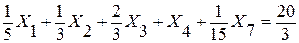 3
3
Данное решение не является оптимальным, так как имеются отрицательные коэффициенты при небазисных переменных в строке 0.
Итерация 2
Для того чтобы улучшить решение, выбираем переменную, которая обеспечивает наибольшее удельное приращение для значения целевой функции. Такой переменной является Х1, так как её коэффициентом (-9/5) является наибольшим по модулю из всех отрицательных коэффициентов. Для выбора разрешающей строки определяем отношения свободных членов к коэффициентам при Х 1.
Строка 1: 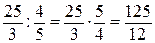 ,
,
строка 2: 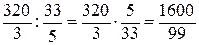 ,
,
строка 3: 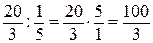 .
.
Наименьшим является значение для строки 1, следовательно переменную Х1 будем переводить в базисную. Для этого в строке 1 коэффициент при Х1 делаем равным 1 (делим уравнение на 4/5)
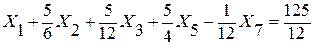 строка 1,
строка 1,
а в остальных строках равным 0:
строка 1´9/5 + строка 0;
строка 1´(-33/5) + строка 2;
строка 1´(-1/5) + строка 3.
Система уравнений примет вид:
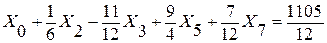 строка 0
строка 0
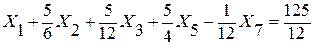 1
1
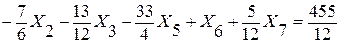 2
2
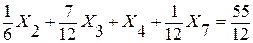 3
3
Решение опять не является оптимальным, так как в нулевой строке есть отрицательный коэффициент при Х3.
Итерация 3
Решение может быть улучшено за счет Х3. Определяем отношения свободных членов уравнений 1, 2, 3 к коэффициентам при Х3:
строка 1: 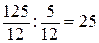 ,
,
строка 2: коэффициент при Х 3 отрицательный,
строка 3: 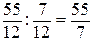 .
.
Следовательно, разрешающим уравнением будет уравнение 3. Преобразуем его так, чтобы коэффициент при Х3 был равен 1. Для этого разделим уравнение на 7/12.
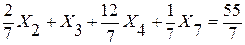 - строка 3.
- строка 3.
Далее исключим переменную Х3 из уравнений 0, 1, 2:
строка 3´11/12 + строка 0;
строка 3´(-5/12) + строка 1;
строка 3´13/12 + строка 2.
Получаем систему:
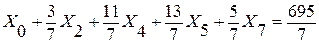 строка 0
строка 0
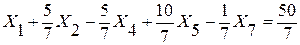 1
1
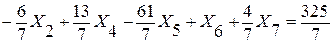 2
2
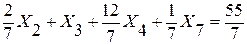 3
3
Итерация 4
Так как в строке 0 все коэффициенты положительные, то полученное решение является оптимальным, то есть
Х0 = 695/7, Х1 = 50/7, Х2 = 0, Х3 = 55/7, Х4 = 0, Х5 = 0, Х6 = 325/7, Х7 = 0.
После преобразования строки 0 в целевую функцию имеем
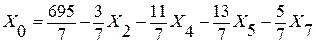 .
.
При любом отличном от нуля значении хотя бы одной из небазисных переменных Х2, Х4, Х5, Х7 целевая функция принимает значение меньше 695/7.
Решение симплекс-методом удобно представлять в виде табл. 2.
Первая итерация соответствует исходной системе уравнений. Для следующей итерации выбираем ведущий элемент, который находится на пересечении столбца с наибольшим по модулю коэффициентом со строкой 0. В данном случае это элемент Х4. Для определения разрешающей строки находим отношения столбца пробных значений к столбцу элемента Х4 (строку 0 из рассмотрения исключаем). Наименьшее отношение соответствует строке 3, следовательно, она и выбирается за разрешающую (в таблице выделено жирным шрифтом).
Вторая итерация получается делением строки 3 на 15. Нулевая строка получается умножением элементов новой строки 3 на 11 и сложением со строкой 0 из первой итерации. Первая строка получается умножением элементов строки 3 из второй итерации на (-1) и сложением её со строкой 1 из первой итерации. Вторая строка получается умножением элементов строки 3 из второй итерации на (-2) и сложением её со строкой 2 из первой итерации. Выбираем ведущий элемент и разрешающую строку во второй итерации. Таким элементом будет элемент Х1 = -9/5 и строка 2, так как отношение 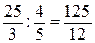 наименьшее.
наименьшее.
Таблица 2
Симплекс-таблица
| Итерация | Базис | Пробные значения | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Строки |
| Х0 Х5 Х6 Х7 | -4 | -5 | -9 | -11 15 | - - - | - - - | - - - | |||
| Х0 Х5 Х6 Х4 | 220/3 25/3 320/3 20/3 | -9/5 4/5 33/5 1/5 | -4/3 2/3 13/3 1/3 | -5/3 1/3 5/3 2/3 | - - - | - - - | - - - | 11/15 -1/15 -2/15 1/15 | ||
| Х0 Х1 Х6 Х4 | 1105/12 125/12 455/12 55/12 | - - - | 1/6 5/6 -7/6 1/6 | -11/12 5/12 -13/12 7/12 | - - - | 9/4 5/4 -33/4 -1/4 | - - - | 7/12 -1/12 5/12 1/12 | ||
| Х0 Х1 Х6 Х3 | 695/7 50/7 325/7 55/7 | - - - | 3/7 5/7 -6/7 2/7 | - - - | 11/7 -5/7 13/7 12/7 | 13/7 10/7 -61/7 -3/7 | - - - | 5/7 -1/7 4/7 1/7 |
Третья итерация получается делением первой строки во второй итерации на 4/5. Результат записывается в первой строке третьей итерации. Нулевую строку в третьей итерации получаем умножением первой строки в этой итерации на 9/5 и сложением с нулевой строкой во второй итерации. Вторую строку получаем умножением первой строки в третьей итерации на (-33/5) и сложением её со второй строкой во второй итерации. Третью строку получаем умножив первую строку в третьей итерации на (-1/5) и сложив её со строкой 3 из второй итерации. Так как в нулевой строке третьей итерации есть отрицательный коэффициент при переменной Х3, то решение не является оптимальным и следует продолжить процедуру итераций до тех пор пока все коэффициенты при переменных в нулевой строке не примут положительное значение. В данном случае это будет четвертая итерация со значением целевой функции 695/7.
 2015-08-21
2015-08-21 391
391







