Вычислительная схема симплекс-метода

Пусть дана задача ЛП в общем виде (ограничения в виде равенства и неравенства).

1. Приведение задачи ЛП к каноническому виду, все ограничения записываются в виде равенств, целевая функция включается в состав ограничений.

2. Получение начального базиса.

3. Проверка условия оптимальности. В случае неоптимальности полученного базисного решения, выбрать номер главного столбца 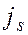. Для этого определяем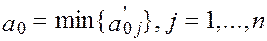

Возможны случаи:

– если 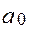>0, то оптимальный базис получен, и задача ЛП имеет единственное решение

– если 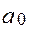=0, то оптимальное решение также получено. В этом случае задача ЛП имеет множество решений

– если 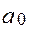<0, то номер столбца, соответствующего 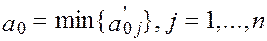, будет номером главного столбца