2015-08-21
579
Положим основные и избыточные переменные равными нулю, тогда остаточные и искусственные переменные будут равны правым частям ограничений. Таким образом, мы сразу получаем первое опорное решение.
Алгоритм симплекс-метода является итерационной процедурой, начиная с опорного решения через ряд промежуточных симплекс-таблиц, приходим к оптимальному решению.
Опорное решение предполагает, что остаточные переменные приравниваются ресурсам, а основные переменные равны нулю.
Коэффициенты индексной строки вычисляются по формуле:
; 
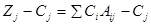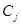- коэффициенты при неизвестных в уравнении для целевой функции;
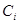- оценка целевой функции;
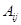- коэффициенты ограничений;
Если среди дополнительных переменных есть только остаточные, то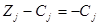 
, т. к. 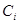=0, т. е. каждый j -ый элемент индексной строки равен взятому с обратным знаком коэффициенту при соответствующей переменной в целевой функции.
Значение целевой функции при этом равно 0,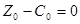 
.
Решение оптимально, когда все элементы индексной строки положительны в задачах на максимум; (отрицательны в задачах на минимум).
В каждой итерации одна переменная вводится в базис – у которой в индексной строке наибольший по абсолютной величине отрицательный элемент (в задачах на минимум – наибольший положительный элемент). Соответствующий столбец называется ключевым (главным, разрешающим).
Увеличивая соответствующую небазисную переменную, в данном примере это X3,, вводя ее в базис, мы увеличиваем значение Z. Для определения выводимой из базиса переменной поочередно разделим значения элементов столбца свободных членов Aio на соответствующие положительные элементы ключевого столбца Aio/Aiкл..
Формирование исходной матрицы в общем виде
Таблица 20
| № ограничений | Базисн. переменные | Оценка целевой функц.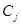
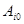|  значение базисной переменной
| 
| 
| 
| 
| 
| 
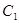
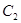
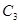
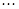
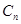
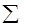
| Контроль | Частное от деления | |||||
| Коэффициенты замещения | ||||||||||||||||
| Основные переменные | Дополнительные переменные | |||||||||||||||
| 
| 
|
| 
| 
| 
| 
|
| 
| |||||||
|
| 
| 
| 
| 
|
| 
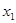
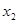
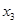
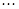
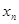
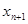
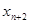
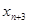
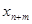
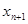
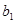
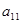
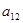
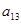
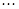
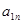
| +1 | |||||||||
|
| 
| 
| 
| 
|
| 
| ||||||||||
|
| 
| 
| 
| 
|
| 
| ||||||||||
|
| 
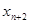
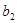
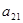
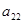
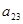
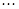
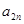
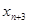
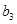
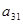
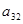
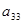
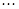
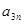
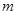
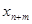
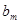
| Коэффициенты при неизвестных в системе ограничений основных элементов. Единичная матрица | |||||||||||||
| Индексная строка |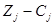 
| 
| 
| 
|
| 
|
|
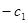
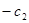
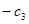
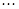
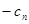
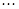
Таблица 21
Первая симплекс-таблица (первое опорное решение).
| № огр. | Баз.переменные. | Оценка цел.функции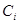
| Значение баз. пер. Аiо |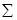 
| Контроль | Частное от деления | ||||||||
| Коэффициенты замещения | ||||||||||||||
| Основные перемен. | Дополнит. перемен. | |||||||||||||
| Х1 (осн) | Х2 (осн) | Х3 (осн) | Х4 (осн) | Х5 (ост) | Х6 (ост) | Х7 (ост) | Х8 (ост) | |||||||
| Х5(ост.) | - | |||||||||||||
| Х6(ост.) | ||||||||||||||
| Х7(ост.) | ||||||||||||||
| Х8(ост.) | -6 | -50 | 60min | |||||||||||
| zj – cj | -100 | -650 | -320 | -1070 | - |
Таблица 22
Вторая симплекс-таблица
| № огр.. | Баз. переменные | Оценка цел.функции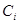
| Значение баз. пер. Аiо |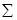
| Контроль | Частное от деления | ||||||||
| Коэффициенты замещения | ||||||||||||||
| Основные перемен. | Дополнит. перемен. | |||||||||||||
| Х1 (осн) | Х2 (осн) | Х3 (осн) | Х4 (осн) | Х5 (ост) | Х6 (ост) | Х7 (ост) | Х8 (ост) | |||||||
| Х5(ост.) | ||||||||||||||
| Х6(ост.) | -1 | |||||||||||||
| Х7(ост.) | 5,9 | 5,2 | -0,5 | |||||||||||
| Х3(осн.) | -0,12 | -1 | 0,2 | 0,02 | 60,1 | - | ||||||||
| zj – cj | -178 | -650 | -190 | - |
Таблица 23
Третья симплекс-таблица
| № огр.. | Баз. переменные | Оценка цел.функции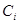
| Значение баз. пер. Аiо |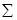
| Контроль | Частное от деления | ||||||||
| Коэффициенты замещения | ||||||||||||||
| Основные перемен. | Дополнит. перемен. | |||||||||||||
| Х1 (осн) | Х2 (осн) | Х3 (осн) | Х4 (осн) | Х5 (ост) | Х6 (ост) | Х7 (ост | Х8 (ост) | |||||||
| Х5(ост.) | 327,3 | 0,8 | -1,64 | -0,018 | 0,018 | 327,46 | ||||||||
| Х2(осн.) | 672,7 | 0,2 | 1,64 | 0,018 | -0,018 | 675,54 | ||||||||
| Х7(ост.) | -2,12 | -60,3 | -0,73 | 0,25 | - | |||||||||
| Х3(осн.) | 732,7 | 0,08 | 1,84 | 0,018 | 0,018 | 735,656 | ||||||||
| zj – cj | -48 | 1,18 | 1,18 |
Таблица 24
Результаты решения симплексной задачи
(Максимизация целевой функции)
| № огр.. | Баз. переменные | Оценка цел.функции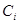
| Значен. базис. пер. Аiо |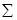
| Контроль | ||||||||
| Коэффициенты замещения | |||||||||||||
| Основные перемен. | Дополнит. перемен. | ||||||||||||
| Х1 (осн) | Х2 (осн) | Х3 (осн) | Х4 (осн) | Х5 (ост) | Х6 (ост) | Х7 (ост) | Х8 (ост) | ||||||
| Х1(осн) | 409,1 | -2,05 | 1,25 | -0,023 | 0,023 | 409,3 | |||||||
| Х2(осн.) | 590,9 | 2,05 | -0,25 | 0,023 | -0,023 | 593,7 | |||||||
| Х7(ост.) | -64,6 | 2,65 | -0,775 | 0,295 | 92457,57 | ||||||||
| Х3(осн.) | -0,1 | 0,02 | 702,92 | ||||||||||
| zj – cj | 10,7 | 2,27 | |||||||||||
Строка, в которой частное от деления оказалось минимальным, называют ключевой (главной) строкой и соответствующая ей базисная переменная выводится из базиса.
Переменная X8 подлежит выводу из базиса в нашем примере. Элемент, находящийся на пересечении ключевого столбца и ключевой строки, называют ключевым (разрешающим).
