Транспортная задача – это задача о наиболее экономном плане перевозок однородного или взаимозаменяемого груза из пунктов производства (со станций отправления) в пункты потребления (на станции назначения).
Транспортная задача может быть сформулирована следующим образом. Некоторый однородный продукт или набор взаимозаменяемых продуктов производится в т пунктах производства 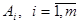 . Задан объем производства
. Задан объем производства 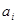 пункта
пункта 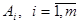 . Произведенный продукт должен быть перевезен в п пунктов потребления
. Произведенный продукт должен быть перевезен в п пунктов потребления 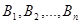 . Известен спрос
. Известен спрос 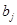 пункта
пункта 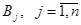 . Заданы также транспортные издержки
. Заданы также транспортные издержки 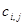 , связанные с перевозкой единицы продукта из пункта
, связанные с перевозкой единицы продукта из пункта 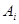 в пункт
в пункт 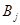 ,
, 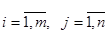 . Требуется составить план перевозок, обеспечивающий при минимальных транспортных издержках удовлетворение спроса всех пунктов потребления за счет продукта, произведенного в пунктах производства. При этом будем считать, что полное предложение в точности равно полному спросу, то есть
. Требуется составить план перевозок, обеспечивающий при минимальных транспортных издержках удовлетворение спроса всех пунктов потребления за счет продукта, произведенного в пунктах производства. При этом будем считать, что полное предложение в точности равно полному спросу, то есть
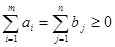 . (1)
. (1)
Обозначим через 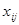 объем продукта, перевозимого из пункта
объем продукта, перевозимого из пункта 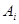 в пункт
в пункт 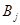 ,
, 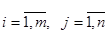 . Тогда математическая модель транспортной задачи принимает следующий вид:
. Тогда математическая модель транспортной задачи принимает следующий вид:
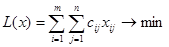 (2)
(2)
при условиях
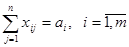 , (3)
, (3)
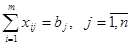 , (4)
, (4)
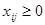 ,
, 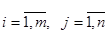 . (5)
. (5)
Теорема. Задача (2)-(5) тогда и только тогда имеет оптимальное решение, когда выполняется условие (1).
Доказательство. Необходимость. Пусть 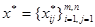 – оптимальное решение задачи (2)-(5). Тогда
– оптимальное решение задачи (2)-(5). Тогда
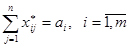 , (6)
, (6)
и
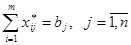 . (7)
. (7)
Складывая т равенств (6) получим 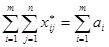 . От сложения п равенств (7) имеем
. От сложения п равенств (7) имеем 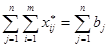 . Так как
. Так как 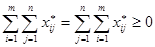 , то и
, то и 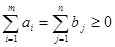 , что и доказывает необходимость условия (1) для существования оптимального решения задачи (2)-(5).
, что и доказывает необходимость условия (1) для существования оптимального решения задачи (2)-(5).
Достаточность. Пусть 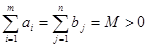 (при М = 0 единственным допустимым, а следовательно, и оптимальным решением транспортной задачи является нулевое решение). Покажем сначала, что
(при М = 0 единственным допустимым, а следовательно, и оптимальным решением транспортной задачи является нулевое решение). Покажем сначала, что 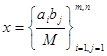 – допустимое решение задачи (2)-(5). Действительно,
– допустимое решение задачи (2)-(5). Действительно, 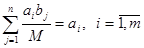 ,
, 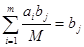 ,
, 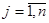 , и
, и 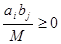 ,
, 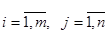 . Таким образом, допустимое множество, определяемое ограничениями (3)-(5), не пусто. Кроме того, оно замкнуто и ограничено. Следовательно, непрерывная функция
. Таким образом, допустимое множество, определяемое ограничениями (3)-(5), не пусто. Кроме того, оно замкнуто и ограничено. Следовательно, непрерывная функция 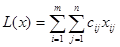 достигает на этом множестве своего минимального значения. Теорема доказана.
достигает на этом множестве своего минимального значения. Теорема доказана.
Задачи, в которых условие (1) соблюдается, называются сбалансированными. Если же условие (1) не выполнено, то задача (2)-(5) не имеет решения и оптимальный план перевозок может быть найден только в том случае, если ограничения (3)-(4) ослаблены, то есть заменены неравенствами. А именно, в случае 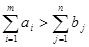 ограничения (3) заменяются неравенствами
ограничения (3) заменяются неравенствами
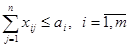 . (8)
. (8)
При решении задачи (2), (8), (4), (5) вводится фиктивный потребитель с потребностью, равной 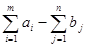 , и тарифами
, и тарифами 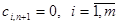 . В этой новой задаче полное предложение и полный спрос равны между собой. С другой стороны, любое оптимальное решение новой задачи дает минимум стоимости для первоначальной задачи. Если же
. В этой новой задаче полное предложение и полный спрос равны между собой. С другой стороны, любое оптимальное решение новой задачи дает минимум стоимости для первоначальной задачи. Если же 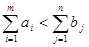 , то ограничения (4) заменяются неравенствами
, то ограничения (4) заменяются неравенствами 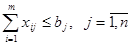 , а для решения задачи вводится фиктивный отправитель с запасом груза
, а для решения задачи вводится фиктивный отправитель с запасом груза 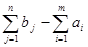 , и тарифами
, и тарифами 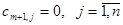 .
.
Запишем более подробно ограничения (3)-(4):

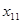
| 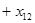
| 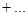
| 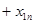
| 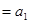
| |||||||||
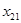
| 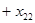
| 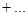
| 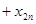
| 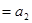
| |||||||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … |
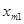
| 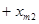
| 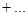
| 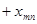
| 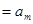
| |||||||||
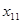
| 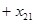
| 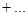
| 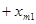
| 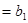
| |||||||||
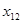
| 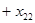
| 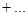
| 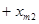
| 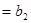
| |||||||||
| … | … | … | … | … | … | … | … | … | … | … | … | … | … |
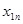
| 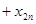
| 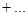
| 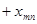
| 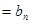
|
Задача, двойственная к (2)-(5), может быть сформулирована так:
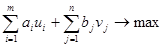 при условии, что
при условии, что 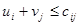 ,
, 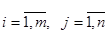 .
.
Из теоремы двойственности и теоремы равновесия вытекает следующее утверждение, полное доказательство которого предлагается провести самостоятельно.
Теорема. Допустимое решение 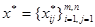 задачи (2)-(5) является ее оптимальным решением в том и только в том случае, если существуют числа
задачи (2)-(5) является ее оптимальным решением в том и только в том случае, если существуют числа 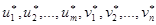 (потенциалы пунктов производства и пунктов потребления), удовлетворяющие условиям:
(потенциалы пунктов производства и пунктов потребления), удовлетворяющие условиям: 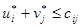 ,
, 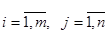 ,
, 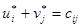 при
при 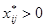 .
.
Один из важнейших результатов, полученных в теории транспортных задач, состоит в том, что среди всех оптимальных решений задачи (2)-(5) существует по крайней мере одно решение, в котором все значения 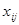 имеют целые значения, если все
имеют целые значения, если все 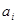 и
и 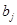 – целые числа. Доказательство этого утверждения можно найти, например, в монографии С.А.Ашманова «Линейное программирование» (М.: Наука, 1981). Таким образом, в предположении, что
– целые числа. Доказательство этого утверждения можно найти, например, в монографии С.А.Ашманова «Линейное программирование» (М.: Наука, 1981). Таким образом, в предположении, что 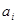 и
и 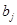 – неотрицательные целые числа, добавление к ограничениям (3)-(5) условия целочисленности
– неотрицательные целые числа, добавление к ограничениям (3)-(5) условия целочисленности 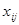 ,
, 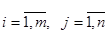 , не оказывает влияния на оптимум задачи (2)-(5).
, не оказывает влияния на оптимум задачи (2)-(5).
Так как транспортная задача является частным случаем задачи линейного программирования, то ее можно решать общими методами линейного программирования. Однако с использованием специфики ограничений (3)-(4) разработаны специальные методы решения транспортной задачи (например, метод потенциалов). Эти методы, в частности, обладают следующим полезным свойством: если при целых 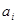 и
и 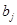 начать решение с некоторого допустимого плана перевозок, в котором все
начать решение с некоторого допустимого плана перевозок, в котором все 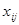 ,
, 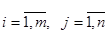 , – целые числа, то в результате применения соответствующего алгоритма мы придем к оптимальному плану перевозок, который также будет удовлетворять требованиям целочисленности. Таким образом, решая задачу (2)-(5) с целочисленными исходными данными, мы автоматически получаем решение задачи (2)-(5) с дополнительным ограничением целочисленности
, – целые числа, то в результате применения соответствующего алгоритма мы придем к оптимальному плану перевозок, который также будет удовлетворять требованиям целочисленности. Таким образом, решая задачу (2)-(5) с целочисленными исходными данными, мы автоматически получаем решение задачи (2)-(5) с дополнительным ограничением целочисленности 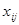 ,
, 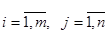 .
.
 2015-08-21
2015-08-21 510
510






