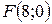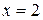Здесь мы дадим еще один подход к изучению эллипса, гиперболы и параболы. Он был известен уже древним грекам до начала нашей эры. Эти кривые можно определить как линии пересечения кругового конуса, или точнее, поверхности кругового конуса, с плоскостью, не проходящей через вершину конуса. Отсюда и происходит их название «конические сечения».
Л.С. Понтрягин (1908 – 1988)
Призма переходит в генератрису, генератриса превращается в касательную, касательная съеживается в лемнискату, лемниската распадается на две окружности, одна из них вытягивается в эллипс, эллипс развертывается в параболу, парабола закручивается в спираль, спираль тихонько обвивает мозг, ее когда-то раскрутивший…
Мигель Отеро Сильва ((Miguel Otero Silva, 1908 – 1985),
«Когда хочется плакать, не плачу»
Конические сечения – линии пересечения прямого кругового конуса с плоскостями, не проходящими через его вершину.
|
В зависимости от взаимного расположения конуса и секущей плоскости получают три типа конических сечений:
– секущая плоскость пересекает все образующие конуса в точках одной его плоскости (рис. 3.6.1 а); линия пересечения – замкнутая овальная кривая – эллипс; окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса;
– секущая плоскость параллельна одной из касательных плоскостей конуса (рис. 3.6.1. б); в сечении получается незамкнутая, уходящая в бесконечность кривая – парабола, целиком лежащая на одной полости;
– секущая пересекает обе полости конуса
(рис. 3.6.1. в) линия пересечения – гипербола – состоит из двух одинаковых незамкнутых, простирающихся в бесконечность частей (ветвей гиперболы), лежащих на обеих полостях конуса.
С точки зрения аналитической геометрии конические сечения – действительные, нераспадающиеся линии второго порядка.
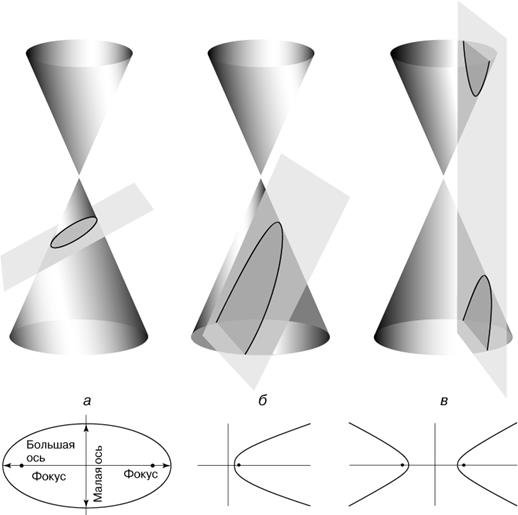
Рис. 3.6.1. Конические сечения как результат пересечения плоскости с конусом.
Конические сечения были известны уже математикам Древней Греции. Менехм ( , ок. 340 до н.э.) открыл, что эллипс, гипербола и парабола являются сечениями конуса. Наиболее полным сочинением, посвященным этим кривым, были «Конические сечения» Аполлония Пергского (
, ок. 340 до н.э.) открыл, что эллипс, гипербола и парабола являются сечениями конуса. Наиболее полным сочинением, посвященным этим кривым, были «Конические сечения» Аполлония Пергского (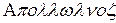 , ок. 262 до н.э. – ок. 190 до н.э.). Дальнейшие успехи теории конических сечений связаны с созданием в ХVII веке новых геометрических методов: проектного (Ж. Декарт, Б Паскаль) и в особенности координатного (Р. Декарт, П Ферма).
, ок. 262 до н.э. – ок. 190 до н.э.). Дальнейшие успехи теории конических сечений связаны с созданием в ХVII веке новых геометрических методов: проектного (Ж. Декарт, Б Паскаль) и в особенности координатного (Р. Декарт, П Ферма).
При определенном выборе системы координат (ось абсцисс – ось симметрии конического сечения, ось ординат – касательная к вершине конического сечения) уравнение конического сечения может быть приведено к виду
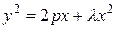 ,
,
где  и
и 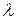 - постоянные,
- постоянные,  .
.
При  уравнение определяет параболу:
уравнение определяет параболу:  , при
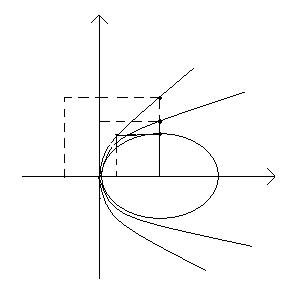
, при 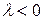 – эллипс, при
– эллипс, при  – гиперболу.
– гиперболу.
  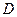 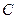 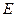 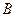 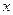 0 0 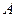 Рис.3.6.2. Рис.3.6.2. |
В переводе с др. греческого парабола означает – приложение, эллипс – недостаток (приложение с недостатком), гипербола – избыток (приложение с избытком). Эти названия возникли, потому что в греческой геометрии превращение прямоугольника, площадь которого равна 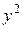 , в прямоугольник такой же площади с основанием
, в прямоугольник такой же площади с основанием 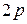 назывался приложением данного прямоугольника к этому основанию (рис. 3.6.2).
назывался приложением данного прямоугольника к этому основанию (рис. 3.6.2).
Создание Р. Декартом в ХVII веке координатного метода позволило от стереометрических определений конических сечений перейти к планиметрическим определениям этих кривых как множеств точек на плоскости.
Коническое сечение – множество точек, для каждой из которых отношение расстояний до данной точки (фокуса) к расстоянию до данной прямой (директрисы) равно данному положительному числу (эксцентриситету)  . При
. При 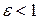 коническое сечение – эллипс; при
коническое сечение – эллипс; при 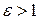 – гипербола; при
– гипербола; при 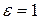 – парабола.
– парабола.
Конические сечения часто встречаются в геометрических описаниях различных явлениях природы и человеческой деятельности. В науке конические сечения приобрели особое значение после того, как И. Кеплер (Kepler, Johann, 1609) открыл из наблюдений, а И. Ньютон (Isaac Newton, 1687) теоретически обосновал законы движения планет.
Пример 3.6.1. Составить уравнение линии, расстояние каждой точки которой от точки 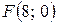 вдвое больше, чем от прямой
вдвое больше, чем от прямой 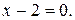 Сделать чертеж.
Сделать чертеж.
Решение. Пусть 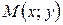 – текущая точка линии. По условию задачи
– текущая точка линии. По условию задачи 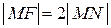 .
.
Тогда
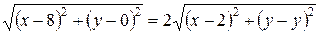 .
.
Возводя в квадрат и раскрывая скобки, получим
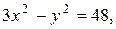 или
или 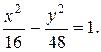
Получено каноническое уравнение гиперболы. Сделаем чертеж (рис. 3.6.3).
| |||
| Рис. 3.6.3. |
Ответ: 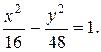
 Пример 3.6.2. Составить уравнение линии, каждая точка которой равноудалена от точки
Пример 3.6.2. Составить уравнение линии, каждая точка которой равноудалена от точки 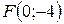 и от прямой
и от прямой 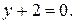 Сделать чертеж.
Сделать чертеж.
Решение. Если 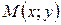 есть текущая точка линии, то по условию задачи
есть текущая точка линии, то по условию задачи 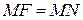 , т.е.
, т.е.
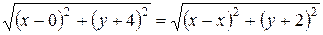 .
. 
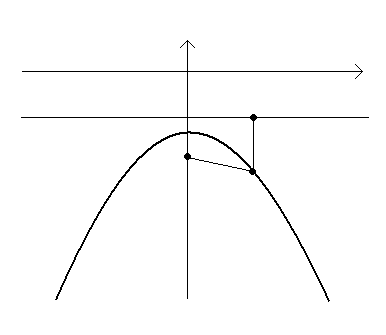 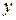 0 0 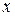  -2 -2 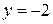 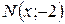 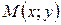 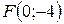 Рис. 3.6.4. Рис. 3.6.4. |
Возведем в квадрат полученное уравнение, после преобразований запишем:
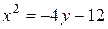 или
или 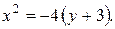
Получим уравнение параболы. Сделаем чертеж (рис. 3.6.4).
Ответ: 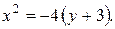
 2015-09-07
2015-09-07 5063
5063
 ) – конус или коническая поверхность – множество прямых (образующих) пространства, соединяющих все точки некоторой линии (направляющей) с данной точкой (вершиной) пространства. Конус визуально состоит из двух полостей (рис. 3.6.1). Простейший конус – круглый или, как его еще называют, прямой круговой конус. Его направляющей линией является окружность, а вершина ортогонально проецируется в центр этой окружности. Осью конуса называется прямая, проходящая через его вершину и центр направляющей окружности.
) – конус или коническая поверхность – множество прямых (образующих) пространства, соединяющих все точки некоторой линии (направляющей) с данной точкой (вершиной) пространства. Конус визуально состоит из двух полостей (рис. 3.6.1). Простейший конус – круглый или, как его еще называют, прямой круговой конус. Его направляющей линией является окружность, а вершина ортогонально проецируется в центр этой окружности. Осью конуса называется прямая, проходящая через его вершину и центр направляющей окружности. 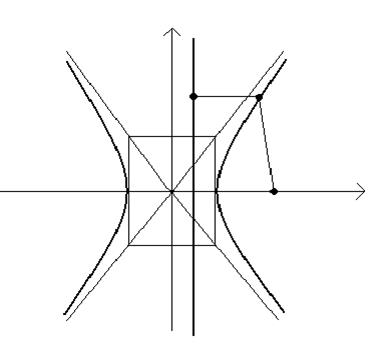
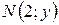
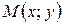 0 2
0 2