Справочный материал

Число всех перестановок без повторений равно: P_n = n!

Число всех размещений без повторений равно:

А 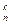= n(n – 1)(n – 2)×××(n – m + 1).

Число всех сочетаний без повторений равно: .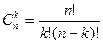

Классическое определение вероятности: Р(А) = .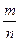

Свойства вероятности:

1⁰. Р(W) = 1, где W - полная группа событий.

2⁰. Вероятность невозможного события равна 0, а достоверного события равна 1. Следовательно, 0 £ Р(А) £ 1.

3⁰. Р(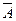) = 1 – Р(А), где 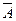и А – противоположные события.

Теорема сложения для двух несовместных событий: Р(А+В) = Р(А)+Р(В), для n попарно несовместных событий:

Р(А₁+А₂+…+А_n) = Р(А₁)+Р(А₂)+…+Р(А_n).

Теорема умножения для двух зависимых событий Р(АВ) = Р(А)×Р(А/В), для n зависимых: Р(А₁А₂×××А_n)=Р(А₁)Р(А₂/A₁)P(A₃/A₁A₂)×××Р(А_n/A₁A₂×××A_n-1).

Теорема умножения для двух независимых событий: Р(АВ) = Р(А)×Р(В), для n независимых: Р(А₁А₂×××А_n)=Р(А₁)Р(А₂)×××Р(А_n).

Вероятность появления хотя бы одного события из n независимых событий А₁, А₂, …, А_n равна: Р(А) = 1 - q₁ q₂ ×××q_n, где р_i = Р(А_i), q _i = 1 – p _i.

Формула полной вероятности: Р(А) = Р(Н₁)Р(А/H₁) + P(H₂)P(A/H₂) + … + +P(H_n)P(A/H_n), где Н_i – попарно-несовместные, образующие полную группу события (гипотезы).

Формула Байеса: Р(А/H _i) = 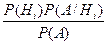, где Р(А) вычисляют по формуле полной вероятности.

Формула Бернулли: Р_n (k)=С 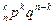, где q = 1 – p.

Наивероятнейшее число появлений k₀ события А в n испытаниях:

np – q 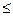k₀ 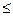np + p.

Локальная теорема Лапласа: P_n(k) 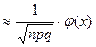, где q = 1-p, х = 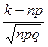, значения функции j(х) см. в таблице приложения 1.

Интегральная теорема Лапласа: Р_n(k₁≤ k ≤ k₂) ≈ Ф(х₂) – Ф(х₁), где х₁ = 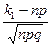, х₂ = 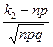, значения функции Ф(х) см. в таблице приложения 2.

Законом распределения дискретной случайной величины:

Х	x1	x2	…	хn
P(X)	p1	p2	…	pn

причем р₁ + р₂ + … + р_n = 1.

Математическое ожидание дискретной случайной величины:

М(Х)=х₁р₁ + х₂р₂ + … +х_np_n.

Дисперсия дискретной случайной величины: D(X) = M(X – M(X))² или более простая формула D(X) = M(X)² – [M(X)]².

Средне квадратическое отклонение: s(Х) = .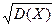

Функцией распределения непрерывной случайной величины (НСВ): F(x) = P (X < x), причем 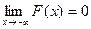и .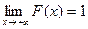

Плотность распределения непрерывной случайной величины: f(x)=F^/(x), следовательно, .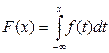

Свойства плотности распределения:

1. f (x) ≥ 0 для всех х.

2. .

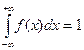Математическое ожидание НСВ: .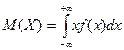

Дисперсия НСВ: D(X)= 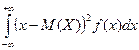или D(X)=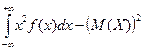

Среднее квадратическое отклонение НСВ: s(Х) = .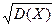

Вероятность того, что нормально распределенная случайная величина примет значение, принадлежащее интервалу (a; b), равна:

Р(a<x<b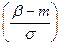) = Ф - Ф 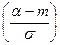, а вероятность того, абсолютная величина отклонения меньше положительного числа d равна: Р(|x – m| < d) = 2Ф .

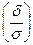Выборочная средняя: 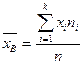, где n=n₁ + n₂ +…+n_k – объем выборки.

Выборочная дисперсия: 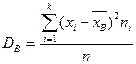, n – объем выборки.

Выборочное среднее квадратическое отклонение: s_В = .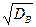

Теорема: D_B= 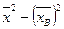, где .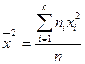

Доверительный интервал, покрывающий неизвестный параметр а (математического ожидания нормального распределения) при известном s, 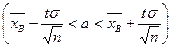где 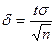- точность оценки, n – объем выборки; t определяют из равенства Ф(t)= 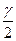(по таблице приложения 2 находят аргумент t, которому соответствует значение функции Лапласа, равное g/2).

Если же s неизвестно, то доверительный интервал, покрывающий неизвестный параметр а с надежностью g, примет вид: 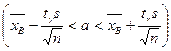, где t_g можно определить по таблице приложения 3 по заданным n и g, s = 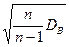- «исправленное» среднее квадратическое отклонение.

Метод произведений. Составляют расчетную таблицу вида:

хi	ni	ui	niui	niu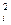

1. В 1^ом столбце записывают выборочные (первоначальные) варианты в возрастающем порядке.

2. Во 2^ом - записывают частоты этих вариант.

3. В 3^ем – записывают условные варианты 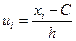(практически, в клетках над u_i=0 по порядку пишут числа -1, -2, -3, …, а в клетках под ним – числа 1, 2, 3, …

4. В 4^ом – вычисляют произведения n_iu_i.

5. В 5^ом – вычисляют произведения n_iu .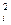

6. Далее суммируют вычисления по столбцам, записывая результаты снизу.

7. Вычисляют условные моменты 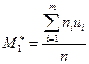, 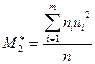и выборочные среднюю 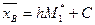, дисперсию 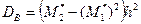и среднее квадратическое отклонение s_В = .

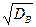Для проверки нулевой гипотезы Н₀={генеральная совокупность распределена нормально} при уровне значимости a с помощью критерия согласия Пирсона удобно пользоваться следующим алгоритмом:

1. Вычисляют теоретические частоты n 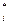= 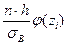, где n – объем выборки; h – шаг выборки; s_В - выборочное среднее квадратическое отклонение; z_i= 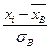( 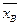- выборочная средняя); j(z)= 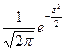- плотность нормированного нормального распределения (значения см. приложение 1).

2. Вычисляют 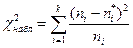( 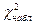- значение критерия, вычисленное по данным наблюдений).

3. По таблице критических точек распределения 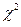(см. приложение 4) по заданному уровню значимости a и числу степеней свободы k = s – 3 (s – число групп выборки) находим 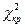(a; k).

4. Если 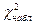< 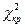, то нет оснований отвергнуть нулевую гипотезу Н₀; если 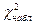> 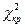, то нулевую гипотезу Н₀ отвергают.

Выборочное уравнение прямой линии регрессии Y на Х по

сгруппированным данным имеет вид: .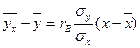

Здесь: 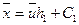, , 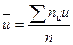h₁ – шаг варианты Х; 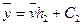, , 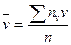h₂ – шаг варианты Y, n – объем выборки; s_х = s_uh₁, s_u = 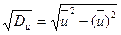, 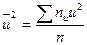; s_y = s_vh₂, s_v = 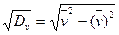, 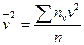; r_B = .

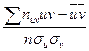Метод нахождения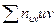

Для этого составляют корреляционную таблицу в условных вариантах, после чего составляют специальную таблицу:

1. В каждой клетке, в которой n_uv ¹ 0, в правом верхнем углу записывают произведение n_uv на u.

2. Складывают все числа, помещенные в этих правых верхних углах и их суммы записывают в столбец U.

3. Умножают варианту v на U по строкам и записывают результаты в последнем столбце vU.

4. Суммируют элементы последнего столбца. Полученная сумма и равна .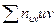

5. Для контроля аналогичные вычисления производят по столбцам (в левых нижних углах клеток, в которых n_uv ¹ 0).