Р А З Д Е Л VII
§1. Базис линейного пространства. Ранг матрицы. Однородные системы линейных уравнений
131. Исследовать систему векторов { 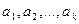 } на линейную зависимость. В случае линейной зависимости данной системы найти линейную комбинацию ее векторов с ненулевыми коэффициентами, равную нулевому вектору (искомая линейная комбинация определена неоднозначно).
} на линейную зависимость. В случае линейной зависимости данной системы найти линейную комбинацию ее векторов с ненулевыми коэффициентами, равную нулевому вектору (искомая линейная комбинация определена неоднозначно).
1) 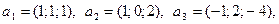
2) 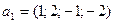 ,
, 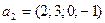 ,
,  ,
, 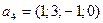 ,
,
3) 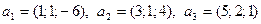 ,
,
4) 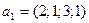 ,
, 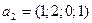 ,
, 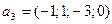 .
.
132. Проверить, что система векторов { 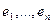 } образует базис линейного пространства
} образует базис линейного пространства 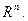 Найти координаты вектора x в этом базисе:
Найти координаты вектора x в этом базисе:
1) 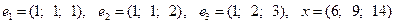 ,
,
2) 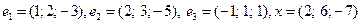 ,
,
3) 
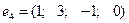 ,
, 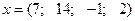 ,
,
4) 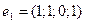 ,
, 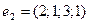 ,
, 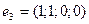 ,
, 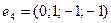 ,
, 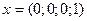 .
.
133. Найти ранг матрицы:
1) 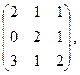 2)
2) 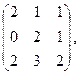 3)
3) 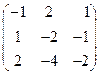 .
.
134. Найти ранг матрицы при различных значениях параметра 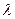 :
:
1) 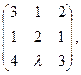
 2)
2) 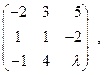 3)
3) 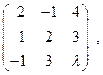
4) 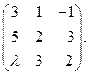
134.1. При каком значении параметра 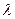 данная матрица является вырожденной
данная матрица является вырожденной
1) 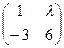 , 2)
, 2) 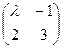 , 3)
, 3) 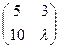 ?
?
134.2. Чему равен ранг матрицы А, если:
1) А – квадратная матрица порядка n и 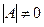 ?
?
2) А – единичная матрица прядка n?
3) А – нулевая матрица 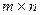 ?
?
4) А – ненулевая квадратная матрица порядка 2 с нулевой строкой?
5) А – ненулевая квадратная матрица порядка 2 и 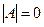 ?
?
6) А – произвольная матрица и 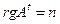 ?
?
134.3. Дайте обоснованные ответы на следующие вопросы:
1) как связаны ранги матриц А и 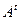 ?
?
2) может ли ранг матрицы размера 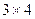 быть равным 4?
быть равным 4?
3) у какой матрицы ранг равен 0?
4) пусть А - квадратная матрица порядка 4 и rgA = 3. Чему тогда равен определитель 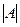 матрицы А?
матрицы А?
5) чему может быть равен ранг вырожденной квадратной матрицы порядка n?
134.4. Доказать теорему Кронекера-Капелли: система линейных уравнений  имеет решение тогда и только тог-да, когда ранг матрицы А системы равен рангу расширенной матрицы
имеет решение тогда и только тог-да, когда ранг матрицы А системы равен рангу расширенной матрицы 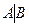 системы, то есть
системы, то есть 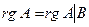 (расширенная матрица
(расширенная матрица 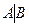 получается из матрицы А приписыванием к ней столбца свободных членов В в качестве последнего столбца).
получается из матрицы А приписыванием к ней столбца свободных членов В в качестве последнего столбца).
135. Найти общее решение однородной системы линейных уравнений и записать его с помощью фундаментальной системы решений (базиса пространства решений однородной системы линейных уравнений):
1) 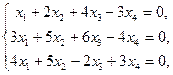 2)
2) 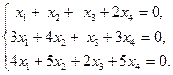
§ 2. Линейные преобразования. Квадратичные формы
Обозначения:
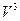 - линейное пространство свободных векторов в пространстве,
- линейное пространство свободных векторов в пространстве,
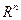 - линейное пространство строк длины n,
- линейное пространство строк длины n,
[ 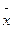 ] - столбец координат вектора
] - столбец координат вектора 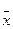 .
.
136. Линейное преобразование  задано формулой
задано формулой 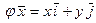
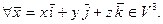 Найти матрицу преобразования
Найти матрицу преобразования  в базисе {
в базисе { 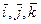 } и образ
} и образ 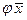 вектора
вектора 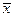 при преобразовании
при преобразовании  , если:
, если:
1) 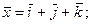 2)
2) 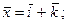 3)
3) 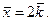
137. Линейное преобразование  задано формулой
задано формулой 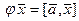 , где
, где 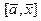 - векторное произведение фиксированного вектора
- векторное произведение фиксированного вектора  на произвольный вектор
на произвольный вектор 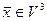 . Найти матрицу преобразования
. Найти матрицу преобразования  в базисе {
в базисе { 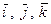 } и образ
} и образ 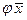 вектора
вектора 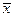 при преобразовании
при преобразовании  , если:
, если:
1)  2)
2) 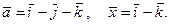
138. Найти матрицу А линейного преобразования 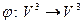 в базисе {
в базисе { 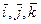 }, если преобразование
}, если преобразование  задано формулой:
задано формулой:
1) 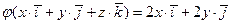 ,
,
 2015-09-07
2015-09-07 364
364






