Основні теоретичні відомості та вказівки

Вектором називається направлений відрізок.

Нехай заданий вектор 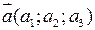. Тоді його абсолютна величина обчислюється за формулою: .

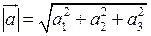Нехай задані точки 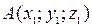та 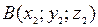. Тоді абсолютна величина вектора 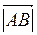обчислюється за формулою:

.

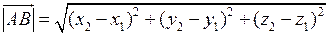Вектор, абсолютна величина (або модуль) якого дорівнює нулю, називається нульовим вектором.

Кожний ненульовий вектор визначається довжиною та напрямком.

Дії над векторами:

Сумою векторів 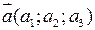та 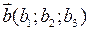називається вектор 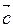з координатами: .

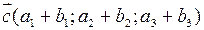Різницею векторів 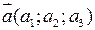та 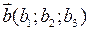називається вектор 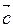з координатами: .

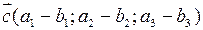Добутком вектора 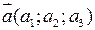на число 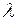називається вектор .

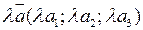Скалярним добутком 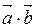векторів 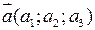та 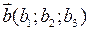називається числ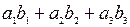о або .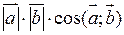

Два ненульових вектори, напрямки яких співпадають або протилежні, називаються колінеарними.

Теорема (ознака колінеарності): Для того, щоб ненульові вектори 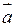та 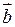були колінеарними, необхідно і достатньо, щоб існувало деяке число 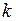, яке задовольняє умові .

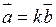Кутом між двома ненульовими векторами називається кут між напрямками цих векторів. Якщо кут між векторами 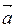та 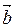дорівнює 90^о, то ці вектори називаються ортогональними (перпендикулярними).

Теорема: Якщо вектори перпендикулярні, то їх скалярний добуток дорівнює нулю.

За визначенням скалярного добутку: 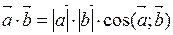. Звідси:

.

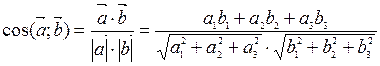Вектори 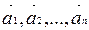називаються компланарними, якщо кожний з них паралельний одній і тій же площині. Будь-які два вектори завжди компланарні.