НФБК (BCNF)

Определение НФБК: отношение находится в нормальной форме Бойса-Кодда, если оно находится в третьей нормальной форме, и каждый детерминант является возможным ключом отношения.

ФИО

Номер зач. кн.

ИД студента

Дисциплина

Дата

Оценка

Это отношение находится в 3НФ, но не находится в НФБК.

НФ

Пример 3. Отношение описывает работу программистов над проектами:

Таб. №

Имя

Зарплата

№ проекта

Дата окончания

Решение проблемы – разбить БД еще:

Таб.№	Имя служ.	Зарпл.		Таб.№	№ проекта		№ проекта	Дата окончания

Пример 4.

Отношение "Абитуриенты-Факультеты-Предметы"

Абитуриент	Факультет	Предмет
Иванов	Математический	Математика
Иванов	Математический	Информатика
Иванов	Физический	Математика
Иванов	Физический	Физика
Петров	Математический	Математика
Петров	Математический	Информатика

Отношение "Абитуриенты"

Номер Абитуриента	Абитуриент
	Иванов
	Петров

Отношение "Факультеты"

Номер Факультета	Факультет
	Математический
	Физический

Отношение "Предметы"

Номер Предмета	Предмет
	Математика
	Информатика
	Физика

Модифицированное отношение "Абитуриенты-Факультеты-Предметы"

Номер Абитуриента	Номер Факультета	Номер Предмета

Определение многозначной зависимости. Пусть 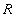- отношение, и 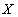, , 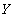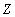- некоторые из его атрибутов (или непересекающиеся множества атрибутов). Тогда атрибуты (множества атрибутов) 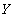и 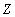многозначно зависят от 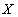(обозначается 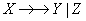), тогда и только тогда, когда из того, что в отношении 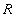содержатся кортеж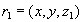и и 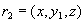следует, что в отношении 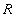содержится также и кортеж к .

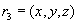Декомпозиция отношения 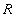на проекци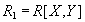и и 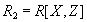будет декомпозицией без потерь тогда и только тогда, когда имеется многозначная зависимость .

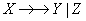Определение 4НФ. Отношение 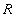находится в четвертой нормальной форме (4НФ), если отношение находится в НФБК и не содержит нетривиальных многозначных зависимостей.

Отношение "Абитуриенты-Факультеты-Предметы" находится в НФБК, но не в 4НФ.

Отношение "Факультеты-Абитуриенты"

Факультет	Абитуриент
Математический	Иванов
Физический	Иванов
Математический	Петров

Отношение "Факультеты-Предметы"

Факультет	Предмет
Математический	Математика
Математический	Информатика
Физический	Математика
Физический	Физика

НФ

Пример 3. Рассмотрим следующее отношение :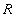

X	Y	Z

Всевозможные проекции отношения 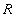, включающие по два атрибута, имеют вид:

Проекция R1=R[X,Y]

X	Y

Проекция R2=R[X,Z]

X	Z

Проекция R3=R[Y,Z]

Y	Z

Отношение 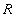не восстанавливается ни по одному из попарных соединени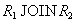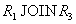й , или 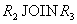. Действительно, соединение 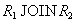имеет вид:

X	Y	Z

Можно предположить, что отношение 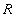в примере 3 удовлетворяет следующей зависимости соединения:

.

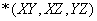Определение нетривиальной зависимости. Зависимость соединения 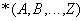называется нетривиальной зависимостью соединения, если выполняется два условия:

· одно из множеств атрибутов 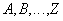не содержит потенциального ключа отношения ;

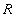• ни одно из множеств атрибутов не совпадает со всем множеством атрибутов отношения .

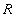Для удобства работы сформулируем это определение так же и в отрицательной форме:

Определение тривиальной зависимости. Зависимость соединения 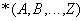называется тривиальной зависимостью соединения, если выполняется одно из условий:

• либо все множества атрибутов 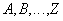содержат потенциальный ключ отношения ;
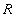• либо одно из множеств атрибутов совпадает со всем множеством атрибутов отношения .

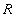Определение 5НФ. Отношение 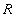находится в пятой нормальной форме (5НФ) тогда и только тогда, когда любая имеющаяся зависимость соединения является тривиальной.

Определения 5НФ может стать более понятным, если сформулировать его в отрицательной форме:

Определение 5НФ. Отношение 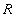не находится в 5НФ, если в отношении найдется нетривиальная зависимость соединения.

Отношение 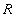находится в пятой нормальной форме (5НФ) тогда и только тогда, когда

любая имеющаяся зависимость соединения является тривиальной.