рациональным уравнениям

О содержании элективного курса, посвященного

И.Л. Мирошниченко

Глазовский государственный педагогический институт им. В.Г. Короленко

С целью систематизации, углубления и обобщения знаний учащихся по методам и приемам решения уравнений и неравенств учителями разрабатываются элективные курсы. Элективный курс по методам решений алгебраических уравнений целесообразно проводить с учащимися десятых классов, тогда останется достаточно времени в 11 классе, для др….В девятилетней школе были рассмотрены линейные, квадратныеТакой элективный курс разработан автором и читается несколько лет учащимся Глазовского района. Обратим внимание на некоторые моменты, касающиеся содержания и методических особенностей данного курса. Позволяет не только углубить и активизировать свои знания,но и развить навыки решения задач, понимать логику их решения логикой математических рассуждений.повысить уровень общей математической подготовки. Эффективные методы решенияРассмотрим наиболее «проблемные»уравнения и неравенства, при решении которых учащиеся чаще всего испытывают затруднения. Задачи при решении которых возникают тонкости…………Тема является актуальнойили …актуальность темы особенно высока в связи с тем что на ЕГЭметодические особенности решения некоторых уравнений и неравенств.

1. Рациональные уравнения и неравенства. Необходимо ввести некоторые сведения из алгебры, такие как теорема Безу и следствия из нее, необходимое условие существования целочисленного корня, показать не только деление многочлена на одночлен (многочлен) углом, но и схему Горнера. На первом этапе рассматриваем приведенные уравнения высших степеней. Полезно рассмотреть уравнения, левая часть которых представляет собой многочлен с целыми коэффициентами и свободным членом равным 1 или -1, которые легко преобразуются в приведенные уравнения с помощью почленного деления на 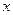в старшей степени (такое деление не приводит к потере корней) и последующей заменой 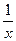на 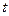. Например, 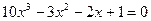, , 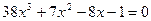, , 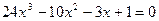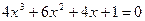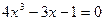. Последние два уравнения можно преобразовать в приведенные, умножив обе части заданного уравнения на такое число, чтобы коэффициент при 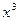стал кубом некоторого целого числа. Умножив обе части уравнения 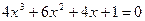на 2, получаем 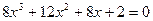. При 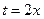, уравнение принимает вид 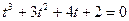. Таким способом можно решать и неприведенные уравнения с любым свободным членом, в которых срабатывает этот прием, например: 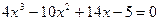, 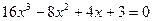. Ясно, что этот способ не является универсальным, поэтому, наконец, можно приступить к решению неприведенных уравнений, рассмотрев теорему о нахождении рациональных корней алгебраических уравнений с целыми коэффициентами. Так же изучаем симметрические и возвратные уравнения, особенности их решения. Известно, что симметрические уравнения четвертой степени, после соответствующих преобразований, с помощью замены 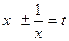сводим к квадратному. Обращаем внимание на важный факт, что при замене 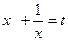, на 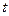можно наложить ограничение: 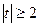(сумма взаимно обратных величин). При решении уравнения вида 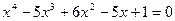такая замена позволяет свести его к квадратному 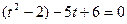(предварительно разделив на 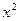и выполнив группировку), корни которого равны 1 и 4. Возвращаясь к переменной 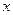, учащиеся в первом случае получают, что уравнение не имеет корней, а при подстановке второго корня, получают 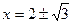. В данном случае, если не принимать во внимание ограничение на 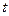, учащиеся теряют незначительную часть времени на решение квадратного уравнения, но при решении уже другого типа заданий этот факт является существенным. Например, такое задание: выясните при каких значениях параметра 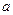уравнение 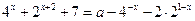имеет решение. Можно сразу ввести замену 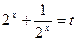, где 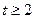, либо в два этапа, сначала 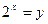, где 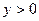, и затем 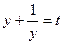, где 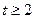. В любом случае мы получаем сумму положительных значений взаимно обратных величин, которая не меньше двух. При решении соответствующего квадратного уравнения учащиеся в лучшем случае считают, что корни должны быть положительными. В статье 34… анализируя типичные ошибки «медальных» работ, автор пишет, что ни один ученик математического класса не использовал этот факт при решении уравнения .

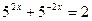2. Квадратный трехчлен. является важнейшей составляющей для подготовки учащихся к экзамену. Знание свойств квадратного трехчлена и умение применять их являются необходимыми условиями успешного выполнения экзаменационной работы. Многочисленные задачи из совсем иных разделов, зачастую сводятся, в конечном итоге, к решению квадратных уравнений или к исследованию квадратного трехчлена. К азбуке квадратного трехчлена относится теорема Виета, которая является мощным инструментом решения многих задач с параметрами. При этом важно помнить, что выполнение соотношений теоремы Виета еще не обеспечивает существование самих корней. Например, требуется найти сумму квадратов корней уравнения 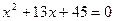. Воспользовавшись теоремой Виета, учащиеся находят, что 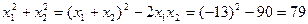, когда сумма квадратов корней исходного уравнения не существует, поскольку не существуют сами корни, так как дискриминант рассматриваемого квадратного трехчлена отрицателен. Решая задачи с параметрами на исследование знаков корней квадратного трехчлена, в первую очередь, рассматриваем задания, в которых нужно найти такие значения параметра, при которых оба корня положительны, отрицательны и только потом, разных знаков. Как правило, учащиеся легко находят условия для первых двух случаев и рассуждая по аналогии выдвигают два условия для третьего случая: первое – условие существования корней (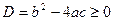) и второе – произведение корней отрицательно (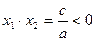). Тогда предлагаем им задание: при каких значениях параметра 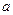квадратный трехчлен 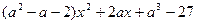имеет корни противоположных знаков. Учащиеся задумываются (не хочется решать громоздкое неравенство пятой степени) и чаще всего с помощью наводящих вопросов приходят к выводу, что так как 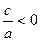, то и 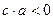, поэтому дискриминант будет положительным и достаточно выполнения только второго условия.

3. Уравнения и неравенства, содержащие знак модуля. В рамках школьного учебника и на уроках математики, видимо в силу объективных причин, не представляется возможным подробно рассмотреть различные способы решения таких задач, в связи с чем, учащиеся недостаточно хорошо ориентируются в выборе эффективного способа решения того или иного уравнения или неравенства в конкретной ситуации.

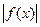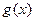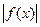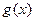
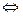
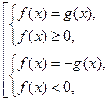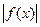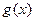
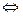
1. Уравнения вида = сводятся к решению совокупности двух систем: = (1) или = 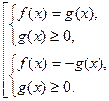(2) (3)

Последнюю совокупность можно заменить системой

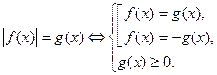(3)

Для каждой схемы равносильности необходимо сформулировать задачу, которая наиболее эффективно решается именно данным способом и требует минимальных затрат времени. Уравнение 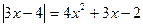целесообразно решать по схеме (1), в чем учащиеся обычно не испытывают трудностей, так как хорошо запоминают алгебраическое определение модуля числа. Для решения уравнения 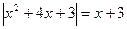оптимальными являются действия по схемам (2) или (3). Если выражения, содержащиеся внутри модуля просты (линейны), рационально применять схему (1), если же функция 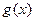проще чем 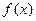, то схему (2). Уравнение 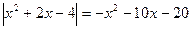удобнее возвести в квадрат, применив формулу разности квадратов, а затем выполнить проверку. Это уравнение было предложено на курсах повышения квалификации учителей математики при МГУ им. Ломоносова и правильно решили эту задачу чуть более 50% слушателей, так как многие применяли традиционный способ раскрытия модуля (1), что приводило к громоздким выкладкам, в которых были допущены ошибки 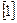. Способ возведения в квадрат эффективен при решении уравнений и неравенств вида: , .

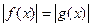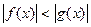2. Практика показывает, что уравнения вида 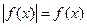, например, 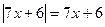учащиеся решают верно, рассуждая: «модуль неотрицательного числа равен самому числу», но при решении уравнений вида 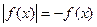, например, 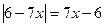, рассуждая: «модуль отрицательного числа равен числу ему противоположному», теряют корень, при котором выражение внутри модуля обращается в нуль. Ошибка является следствием именно такой трактовки определения модуля числа, которое дают авторы некоторых школьных учебников. 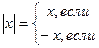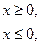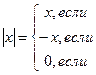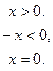Целесообразно вводить определение модуля числа следующим образом: или как в 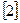или вводить соответствующую словесную формулировку. Это обстоятельство существенно повлияет на темп решения уравнений вида 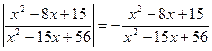и не повлечет потерю корней.

3. Довольно часто встречаются уравнения и неравенства на соотношения с двумя и более переменными, демонстрирующие специальные свойства абсолютной величины числа. Но если учащийся забыл (не знал) их, достаточно внимательно проанализировать структуру задачи, установить связь подмодульных выражений, и, выполнив несложные преобразования выявить условия, при которых она выполняется. При решении неравенства 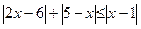заметим, что 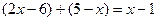. 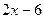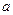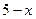Обозначив через , через 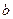получаем неравенство 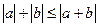, которое в силу свойства 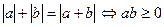равносильно неравенству 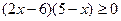. Решая его, получаем 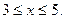Структура этого примера может быть известна многим учащимся, но могут встретиться и совершенно неожиданные для них соотношения. Заметим, что уравнение 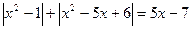имеет вид: 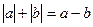. 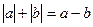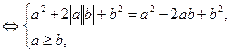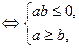Тогда, 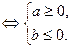Следовательно,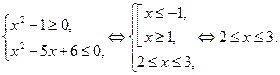

Конечно, последние задачи можно было решить распространенным методом разбиения на промежутки, но он займет гораздо больше времени и вычислений.

Особое внимание уделяем показательным и логарифмическим неравенствамкак с постоянным, так и с переменным основанием. Равносильные преобразования позволяют свести решение, например, неравенства 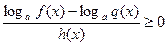или 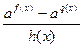к решению рационального неравенства, 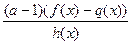которое решается классическим методом интервалов. Рационального неравенства

Литература

1. Потапов, М.К., Шевкин А.В. Итоги одной контрольной работы на курсах повышения квалификации учителей при механико-математическом факультете МГУ // Математика в школе, – 2009. – №10 – С.33-39.

2. Дорофеев, Г.В. Алгебра и начала анализа. 10 кл.: Учеб. для общеобразоват. учреждений: В 2 ч. Ч. 1/Г.В. Дорофеев и др., – 7-е изд.-М.: Дрофа, 2003. – 320 с.

3. Голубев, В.И. Абсолютная величина в конкурсных экзаменах по математике (по материалам ведущих вузов страны) / Львов: Журнал «Квантор». Львов: – 1991. 96с.