Природы

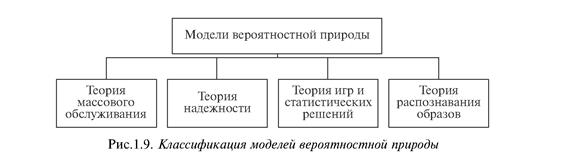
Все кибернетические модели, рассматриваемые в теории ав­томатизированного управления, разделены на три группы. Здесь первую группу составляют модели, в основе которых лежит веро­ятностная природа (рис. 1.9). Это модели теории массового обслу­живания, теории надежности, теории игр, распознавания образов.

Теория массового обслуживания (теория очередей) — это раздел прикладной математики, изучающий процессы, связанные с удо­влетворением массового спроса на обслуживание какого-либо вида с учетом случайного характера спроса и обслуживания (те­лефонные задачи, запасы продуктов, транспортные перевозки, дороги). Теория надежности изучает закономерности возникно­вения и устранения отказов. Теория игр и статистических реше­ний — это математическая теория оптимальных решений в конф­ликтных ситуациях. Теория распознавания образов изучает процессы принятия решений о наиболее существенных свойствах некото­рого объекта на основании косвенных данных, т. е. на основании наблюдения других свойств — признаков, зависящих от упомяну­тых существенных свойств.

Вторая группа объединяет кибернетические модели объектов, поведение которых описывается дифференциальными или раз­ностными уравнениями. Большинство методов исследования та­ких систем излагается в работах по системам автоматического ре­гулирования и управления. Для этих методов характерно рас­смотрение процессов во времени, поэтому такие модели могут быть названы динамическими системами.

Третью группу кибернетических моделей составляют дискрет­ные кибернетические модели. Эти модели применяются и для исследования процессов управления, протекающих во времени, но в основном в них время не используется. Например, требуется с помощью вычислительных машин раскроить листовое железо для обшивки корабля наилучшим образом с точки зрения расхода материала, причем время, в течение которого производится рас­крой, не имеет особого значения. Здесь с успехом применяются как детерминированные, так и вероятностные методы расчета.

В общей структурной схеме математических основ киберне­тики рассматриваются еще специальные прикладные вопросы.