Оптимизация инвестиционного портфеля по модели Шарпа

Выведенные Марковицем правила построения границы эффективных портфелей позволяет находить оптимальный (с точки зрения инвестора) портфель для любого количества ценных бумаг в портфеле. Основной сложностью применения метода Марковица является большой объем вычислений, необходимый для определения весов Wi каждой ненкой бумаги. Действительно, если портфель объединяет n ценных бумаг, то для построения границы эффективных портфелей необходимо предварительно вычислить n значений ожидаемых (средних арифметических) доходностей E(ri) каждой пенной бумаги, n величин s²i дисперсий всех норм отдачи и n(n-1)/2 выражений попарных ковариации sij ценных бумаг в портфеле.

В 1963 г. американский экономист У. Шарп (William Sharpe) предложил новый метод построения границы эффективных портфелей, позволяющий существенно сократить объемы необходимых вычислений. В дальнейшем этот метод модифицировался и в настоящее время известен как одноиндексная модель Шарпа (Sharpe single-index model).

Общее описание модели. В основе модели Шарпа лежит метод линейного регрессионного анализа, позволяющий связать две случайные переменные величины - независимую X и зависимую Y линейным выражением типа Y = a + bхХ. В модели Шарпа независимой считается величина какого-то рыночного индекса. Таковыми могут быть, например, темпы роста валового внутреннего продукта, уровень инфляции, индекс цен потребительских товаров и т.п. Сам Шарп в качестве независимой переменной рассматривал доходность r_m, вычисленную на основе индекса Standart and Poor's (S&P500). В качестве зависимой переменной берется доходность ri какой-то i-ой ценной бумаги. Поскольку зачастую индекс S&P500 рассматривается как индекс, характеризующий рынок ценных бумаг в целом, то обычно модель Шарпа называют рыночной моделью (Market Model), а доходность r_m - доходностью рыночного портфеля.

Пусть доходность r_m принимает случайные значения, и в течение N шагов расчета наблюдались величины r_m1, r_m2, … r_mN. При этом доходность ri какой-то i-ой ценной бумаги имела значения ri1, ri2,…riN. В таком случае линейная регрессионная модель позволяет представить взаимосвязь между величинами r_m и ri в любой наблюдаемый момент времени в виде:

ri,t = ai + bir_m,t + ei,t (4.4)

где; ri,t - доходность i-ой ценной бумаги в момент времени t (например, 31 декабря 2000 года);

ai - параметр, постоянная составляющая линейной регрессии, показывающая, какая часть доходности i-ой ценной бумаги не связана с изменениями доходности рынка ценных бумаг r_m;

bi - параметр линейной регрессии, называемый бета, показывающий чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности;

r_m,t - доходность рыночного портфеля в момент t,

ei,t - случайная ошибка, свидетельствующая о том, что реальные, действующие значения ri,t и rm,t порою отклоняются от линейной зависимости.

Особое значение необходимо уделить параметру bi, поскольку он определяет чувствительность доходности i-ой ценной бумаги к изменениям рыночной доходности.

В общем случае, если bi>l, то доходность данной ценной бумаги более чувствительная, подвержена большим колебаниям, чем рыночная доходность r_m. Соответственно, при bj<1 ценная бумага имеет меньший размах отклонений доходности r_j от средней арифметической (ожидаемой) величины E(r)j, чем рыночная доходность. В этой связи ценные бумаги с коэффициентом b>1 классифицируются как более рискованные, чем рынок в целом, а с b<1 - менее рискованными.

Как доказывают исследования, для большинства ценных бумаг b>О, хотя могут встретиться ценные бумаги и с отрицательной величиной b.

Определение параметров ai и bi регрессионной модели. Для нахождения параметров ai и bi по результатам наблюдений используется метод наименьших квадратов (МНК). По этому методу в качестве параметров ai и bi берутся такие значения, которые минимизируют сумму квадратов ошибок e. Если пронести необходимые вычисления, то окажется, что параметры ai и bi принимают следующие значения:

(4.6)

ai = E(ri) - bi х E(r_m) (4.5)

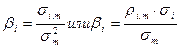Оценка результатов регрессии. Параметры ai и bi регрессионной модели дают представление об общих тенденциях взаимосвязей между изменениями рыночного показателя r_m и нормой отдачи ri. Однако величины ai и bi не позволяют давать однозначный ответ о степени подобной взаимосвязи. На точность регрессионной модели оказывает значительное влияние ошибки ei. Значит, точность регрессионной модели, степень взаимосвязи r_m и ri, определяется разбросим случайных ошибок ei. который можно оценить с помощью дисперсии случайной ошибки s²_ei. Кроме того, точность регрессии можно определить, оценивая, сколь точно регрессионная модель определяет дисперсию s²_i ценных бумаг, для которых составляется регрессионная модель.

Дисперсию i-ой ценной бумаги s²_i можно представить в виде двух слагаемых:

s²_i = b²_i * s²_m + s²_ei

Разделим обе части равенства на величину s²_i:

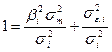В этом случае первое слагаемое будет показывать, какую долю в общем риске ценной бумаги можно описать с помощью регрессионной модели (ri,t = ai + bir_m,t), а второе слагаемое - степень неточности peгрессионной модели. Значит, чем ближе величина b²_is²_m/s²_i ближе к единице, тем более точная регрессионная модель. Если обратиться к равенству, то можно увидеть, что b²_is²_m/s²_i = r²_im.

Следует иметь в виду, что квадрат коэффициента корреляции r²_im является общепризнанной мерой оценки линейной регрессии, то есть мерой того, насколько точно уравнение регрессии подходит для описания соотношений реальных данных ri,t и rm,t.

Поскольку для определения оптимального портфеля с использованием модели Шарпа понадобятся значения дисперсий s²_ei случайных ошибок, то вычислим их. Общая формула для вычисления дисперсии и случайной ошибки имеет вид:

(4.7)

В данном случае средняя арифметическая величина вычисляегся делением на (N-2), поскольку две степени свободы были утеряны при вычислении ai и bi.

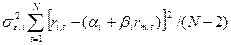Использование рыночной модели Шарпа для построения границы эффективных портфелей. Одно из главных достоинств модели Шарпа состоит в том, что она позволяет значительно сократить объемы вычислений при определении оптимального портфеля, давая при этом результаты, близко совпадающие с получаемыми по модели Марковица. Поскольку в основу модели Шарпа положена линейная регрессия, то для ее применения необходимо ввести ряд предварительных условий. Если предположить, что инвестор формирует портфель из n ценных бумаг, то будем считать, что:

1)Средняя арифметическая (ожидаемая) величина случайных ошибок E(ei)=0 для всех ценных бумаг портфеля, то есть для i = 1, 2,..., n.

2) Дисперсия случайных ошибок s²_ei для каждой ценной бумаги постоянна.

3)Для каждой конкретной ценной бумаги отсутствует корреляция между наблюдаемыми в течение N лет величинами случайных ошибок.

4) Отсутствует корреляция между случайными ошибками любых двух ценных бумаг в портфеле.

5) Отсутствует корреляция между случайными ошибками ei и рыночной доходностью.

Используя эти упрощения, можно получить выражения E(ri), s²_i и si,j для любых ценных бумаг в портфеле:

E(ri) = ai + bi х E(r_m);

s²_i = b²_i * s²_m + s²_ei;

sij = bi bj s²_m

Подведем итог: если инвестор формирует портфель из n ценных бумаг, то использование параметров линейной репрессии ai и bi позволяет выразить с их помощью все начальные элементы - ожидаемую доходность E(ri) каждой ценной бумаги в портфеле, дисперсии s²_i и ковариации ri,j норм отдачи этих ценных бумаг, необходимые для построения границы эффективных портфелей. При этом инвестору требуется предварительно вычислить n значений ai, n величин bi, n значений s²_ei, а также E(r_m) и s²_m. Следовательно всего потребуется найти: (n+n+n+2) = Зn+2 начальных данных, что существенно меньше объема вычислений для модели Марковица.

(4.8)

Определение ожидаемой доходности и дисперсии портфеля. Ожидаемая доходность портфеля, состоящего из n ценных бумаг, вычисляется по формуле

(4.9)

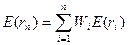где Wi - вес каждой ценной бумаги в портфеле. Подставим в эту формулу выражение для ri:

(4.10)

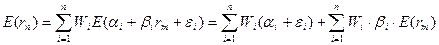Для придания этой формуле компактности, Шарп предложил считать рыночный индекс как характеристику условной (п+1)-ой ценной бумаги в портфеле. В таком случае, второе слагаемое уравнения можно представить в виде:

(4.11)

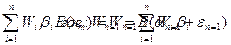a_n+1 + e_n+1 = r_m

при этом считается, что дисперсия (n+1)-ой ошибки равна дисперсии рыночной доходности: s²_e,n+1 = s²_m. Выражение (7.11) представляет собой сумму взвешенных величин "беты" (bi) каждой ценной бумаги (где весом служат Wi) и называется портфельной бетой (bn). С учетом сделанных допущений, формулу (4.8) можно записать так:

(4.12)

(4.13)

а поскольку, согласно введенному начальному условию 1), Е(ei) = 0, то окончательно имеем:

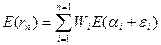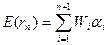Итак, ожидаемую доходность портфеля Е(rn) можно представить состоящей из двух частей:

а) суммы взвешенных параметров ai каждый ценной бумаги – W_1a1+ W_2a2+…+ W_nan, что отражает вклад в Е(rn) самих ценных бумаг, и

б) компоненты W_n+1α_n+1=∑W_iβ_iE(r_m), то есть произведения портфельной беты и ожидаемой рыночной доходности, что отражает взаимосвязь рынка с ценными бумагами портфеля.

(4.14)

Дисперсия портфеля. Дисперсия портфеля в модели Шарпа представляется в виде:

При этом только необходимо иметь в виду, что уравнение (4.11) ______________ то есть (Wn+1)²=(W₁b₁ + W₂b₂ +…+ W_nb_n)², а s²_e,n+1=s²_m. Значит, дисперсию портфеля, содержащего n ценных бумаг, можно представить состоящей из двух компонент:

а) средневзвешенных дисперсий ошибок SW²_is²_e,i, где весами служат Wi, что отражает долю риска портфеля, связанного с риском самих ценных бумаг (собственный риск);

б) b²_ns²_m - взвешенной величины дисперсии рыночною показателя s²_m, где весом служит квадрат портфельной беты, что отражает долю риска портфеля, определяемого нестабильностью самого рынка (рыночный риск).

В модели Шарпа цель инвестора сводится к следующему:

(4.15)

необходимо найти минимальное значение дисперсии портфеля

(4.16)

при следующих начальных условиях:

	(4.17)
		(4.18)

Итак, отметим основные этапы, которые необходимо выполнить для построения границы эффективных портфелей в модели Шарпа:

1) Выбрать n ценных бумаг, из которых формируется портфель, и определить исторический промежуток в N шагов расчета, за который будут наблюдаться значения доходности r_i,t каждой ценной бумаги.

2) По рыночному индексу (например, АК&М) вычислить рыночные доходности rm,t для того же промежутка времени.

3) Определить величины bi:

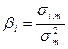4) Найти параметр ai:

α_i=E(r_i) – β_iE(r_m)

5) Вычислить дисперсии s²_ei ошибок регрессионной модели.

6) Подставить эти значения в уравнения (4.15 - 4.18)

После такой подстановки выяснится, что неизвестными величинами являются веса Wi ценных бумаг. Выбрав определенную величину ожидаемой доходности портфеля Е*, можно наши веса ценных бумаг в портфеле, построить границу эффективных портфелей и определить оптимальный портфель.