Теоретические основы работы

ЦЕЛЬ РАБОТЫ

Определение отношения теплоемкостей воздуха с по-мощью уравнений изопроцессов в идеальном газе.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Теплоемкостью тела называется величина, равная отно-шению бесконечно малого количества поглощенной теплоты 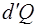к бесконечно малому повышению температуры 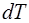, вызванному поглощением этой теплоты:

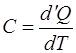. (1.2.1)

Если теплоемкость не зависит от температуры, то из оп-ределения следует, что она численно равна теплоте, погло-щаемой телом при нагревании на единицу температуры.

Теплоемкость единицы массы вещества называется удель-ной теплоемкостью, теплоемкость одного моля вещества – молярной теплоемкостью. Далее будем рассматривать мо-лярные теплоемкости.

Количество теплоты, поглощаемой телом, и, следова-тельно, теплоемкость тела зависят от способа нагревания. Различают теплоемкость при постоянном объеме 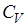и теп-лоемкость при постоянном давлении .

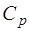По Первому началу термодинамики количество теплоты 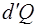, сообщенное термодинамической системе, расходуется на увеличение внутренней энергии системы и совершение системой работы:

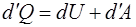, (1.2.2)

где 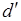означает не приращение какой-либо функции а элементарное количество теплоты 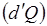и работы .

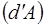При изохорном нагревании газа (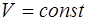) не происходит изменение объема (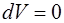), и поэтому работа газа 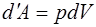тоже равна нулю. Теплота, поглощенная телом, идет только на увеличение внутренней энергии тела (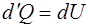). Исходя из этого теплоемкость 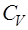равна

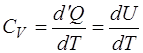. (1.2.3)

При изобарном нагревании (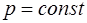) один моль расши-ряющегося газа совершает против внешних сил работу 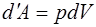. Найдем зависимость работы, совершаемой газом, от изменения температуры. Для этого рассмотрим 1 моль га-за в двух состояниях – до поглощения теплоты (состояние 1) и после поглощения (состояние 2). В состоянии 1 газ имел следующие параметры:

Давление: ,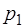

Объем: ,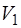

Температура: .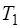

Запишем уравнение Менделеева–Клапейрона для состоя-ния 1:

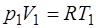, (1.2.4)

где 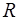– универсальная газовая постоянная.

При переходе в состояние 2 газ при постоянном давле-нии увеличил свой объем на величину 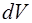и температуру – на 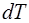. Параметры газа в состоянии 2:

Давление: ,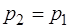

Объем: ,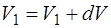

Температура: .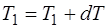

Уравнение Менделеева–Клапейрона для состояния 2:

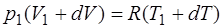(1.2.5)

Вычтем из (1.2.4) выражение (1.2.5)

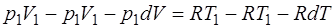
и получим выражение для работы, совершенной газом:

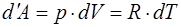. (1.2.6)

Из (1.2.6) виден физический смысл универсальной газо-вой постоянной 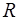: она численно равна работе, совершае-мой 1 молем газа в процессе изобарного расширения при увеличении температуры на 1 кельвин. Разделив 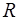на коли-чество молекул в одном моле (число Авогадро 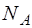), полу-чим работу, совершаемую одной молекулой против внеш-них сил при тех же условиях нагревания. Эта работа чис-ленно равна постоянной Больцмана :

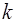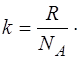(1.2.7)

Подставим полученное выражение для работы (1.2.6) в уравнение Первого начала термодинамики (1.2.2):

,

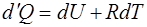и отсюда, с учетом (1.2.1), получаем выражение для тепло-емкости при постоянном давлении:

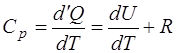. (1.2.8)

Подставляя в (1.2.8) выражение для 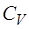, получаем урав-нение

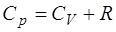, (1.2.9)

называемое уравнением Майера. Из уравнения Майера вид-но, что теплоемкости при постоянном давлении и объеме отличаются на константу. Из этого следует, что и отно-шение теплоемкостей – тоже величина постоянная. Вместе с тем неясно, от чего зависит теплоемкость 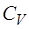. Для того, чтобы вывести уравнение для 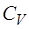, проанализируем выраже-ние (1.2.3), описывающее зависимость 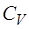от внутренней энергии газа.

Внутренняя энергия газа зависит от числа степеней сво-боды молекул, составляющих газ. Числом степеней свобо-ды системы называется число независимых координат, оп-ределяющих положение системы в пространстве. Моле-кулы, состоящие из различного количества атомов, обла-дают и различным числом степеней свободы 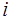. Для одно-атомного газа 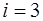, для двухатомного 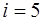, для газа, моле-кулы которого состоят из трех и большего количества ато-мов, .

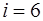Из теоремы о равномерном распределении энергии по степеням свободы следует, что на каждую поступательную и вращательную степень свободы молекулы приходится одинаковая (в среднем) энергия, пропорциональная абсо-лютной температуре газа:

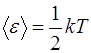. (1.2.10)

Соответственно, если молекула обладает 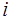степенями сво-боды, то ее кинетическая энергия

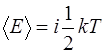. (1.2.11)

Тогда 1 моль идеального газа (газа, в котором можно пре-небречь взаимодействием молекул), состоящий из молекул с 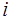степенями свободы, согласно (1.2.7), обладает внутрен-ней энергией

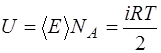. (1.2.12)

Таким образом, для молярной теплоемкости при посто-янном объеме 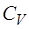получаем выражение, зависящее только от числа степеней свободы молекул газа:

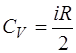. (1.2.13)

Из уравнения Майера получаем выражение для теплоем-кости при постоянном давлении:

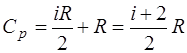. (1.2.14)

Тогда и отношение теплоемкостей есть величина посто-янная, зависящая от числа степеней свободы молекул газа:

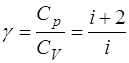. (1.2.15)

Если экспериментально определить величину 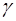, то из (1.2.15) можно найти количество степеней свободы молекул данного газа:

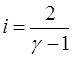. (1.2.16)

Величина 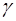является одной из важнейших термодинами-ческих величин, она носит название показателя адиабаты. Адиабатический процесс – это процесс, проходящий без теплообмена со внешней средой (). Состояние иде-ального газа при адиабатическом процессе описывается уравнением Пуассона:

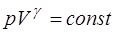. (1.2.17)

Адиабатический процесс тоже относится к изопроцессам, т.к. в отсутствие теплообмена энтропия 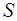системы, опре-деляемая как

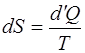(1.2.18)

остается неизменной (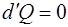, следовательно, ).

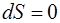Адиабатический процесс еще называется изоэнтропным, или 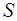-процессом. Энтропия характеризует степень беспо-рядка в системе. Адиабатический процесс занимает особое место в термодинамике. Он характеризует связь между тер-модинамическими параметрами замкнутой макросистемы и поэтому является основой для установления взаимозави-симостей между параметрами. По Первому началу термоди-намики при адиабатическом процессе работа совершается системой за счет внутренней энергии 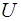. Но если система находится в тепловом равновесии со средой, имеющей тем-пературу 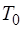, то из энергии системы 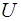в виде работы отда-ется величина, не превышающая 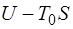. Величина 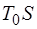на-зывается связанной энергией. Она передается только через теплообмен. Поскольку связанная энергия пропорциональна энтропии, то энтропия характеризует обесцененность энер-гии системы: энтропия возрастает во всех процессах, уменьшающих способность системы производить работу.

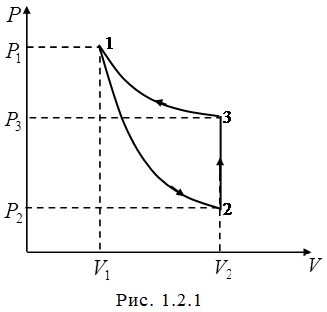
Исходя из физического смысла показателя адиабаты ло-гично сделать вывод, что эксперимент по определению ве-личины 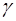должен быть построен так, чтобы термодинами-ческая система хотя бы один раз переходила из состояния в состояние при помощи адиабатического процесса. Кроме того, желательно, чтобы система возвратилась в исходное состояние после прохождения нескольких процессов, т.е. совершила цикл, или круговой процесс. На рис.1.2.1 пред-ставлен такой цикл, состоящий из адиабаты 1-2, изохоры 2-3 и изотермы 3-1.

Состояние идеального газа при изотермическом процессе (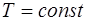) описывается уравнением Бойля-Мариотта

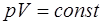. (1.2.19)

С учетом того, что 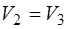, уравнение (1.2.19) для изо-термы 3-1 имеет вид:

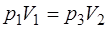. (1.2.20)

Уравнение (1.2.17) для адиабаты 1-2 записывается как:

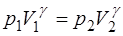. (1.2.21)

Уравнения (1.2.20) и (1.2.21) образуют систему уравне-ний, решая которую, мы найдем величину 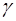. Для этого воз-ведем уравнение (1.2.20) в степень :

,

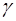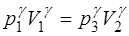и поделим его на уравнение (1.2.21). Получим:

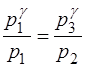, или 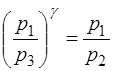. (1.2.22)

Логарифмируя уравнение (1.2.22), получим искомую величину:

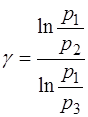, (1.2.23)

где 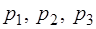– давление газа, соответственно, в состоя-ниях 1,2,3 цикла, указанного на рис.1.2.1.

Выражение (1.2.23) можно упростить, если во время про-ведения цикла давление 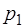и 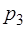незначительно отличается от 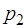. Введем следующие обозначения для давления, пре-вышающего :

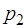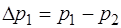; (1.2.24)

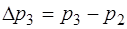. (1.2.25)

Тогда из рис. 1.2.1 следует, что

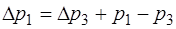. (1.2.26)

Соответственно выражение (1.2.22) для определения γ приобретает вид:

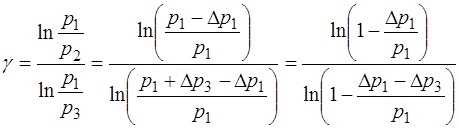. (1.2.27)

Используя разложение функции логарифма в ряд Маклорена и сохраняя только первый член разложения 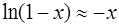из (1.2.27), окончательно получаем

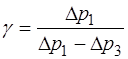. (1.2.28)

Для выяснения физического смысла полученного при-ближения (1.2.28) запишем уравнение изотермы (1.2.19) и адиабаты (1.2.17) в дифференциальном виде:

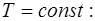
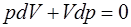; (1.2.29)

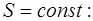
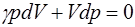. (1.2.30)

Из сравнения формул (1.2.29) и (1.2.30) очевидно, что отношение теплоемкостей 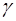может быть найдено как отно-шение угловых коэффициентов адиабаты и изотермы, по-скольку

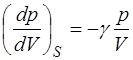, (1.2.31)

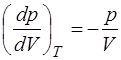. (1.2.32)

Объединяя соотношения (1.2.31) и (1.2.32), получаем ра-венство:

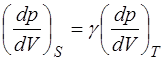, (1.2.33)

которое выполняется при любых заданных значениях 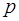и 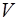. Если по-прежнему считать, что в ходе цикла изменения 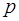и 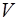малы, то адиабату и изотерму можно с хорошей точ-ностью заменить отрезками прямых, угловые коэффици-енты которых на интервале 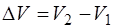соответственно рав-ны:

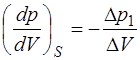, (1.2.34)

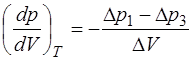(1.2.35)

Таким образом, для отношения теплоемкостей вновь по-лучаем выражение (1.2.28):

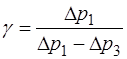, (1.2.36)

которое в работе используется в качестве расчетного.

Преимущество данного подхода и полученного прибли-женного соотношения (1.2.36) заключается в его простоте, высокой точности и возможности измерения давления в произвольных единицах (например в мм водяного столба). В настоящей работе 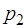равно атмосферному давлению.