1. Найти произведение матриц:
а) 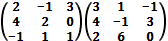
б) 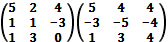
в) 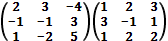
г) 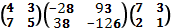
2. Найти значение многочлена 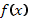 от матрицы
от матрицы 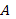 :
:
а) 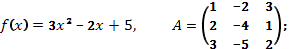
б) 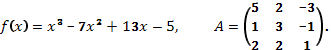
3. Вычислить определитель матрицы путем разложения его по элементам:
а) второй строки:
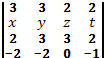
б) третьего столбца:
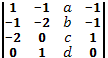
4. Вычислить определитель:
а) 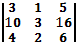
б) 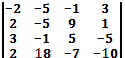
в) 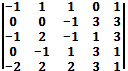
5. По формуле найти обратную матрицу для матрицы:
а) 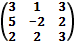
б) 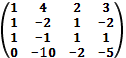
6. С помощью элементарных преобразований строк найти матрицу, обратную к матрице:
а) 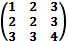
б) 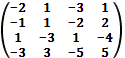
7. Решить матричное уравнение:
а) 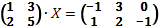
б) 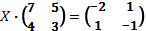
в) 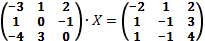
г) 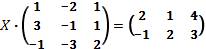
8. Найти ранг матрицы:
а) 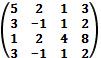
б) 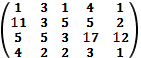
в) 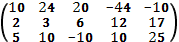
9. Решить систему линейных уравнений по правилу Крамера:
а) 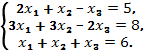
б) 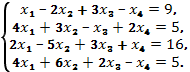
10. Исследовать совместность, найти общее решение и одно частное решение системы уравнений:
a) 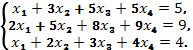
б) 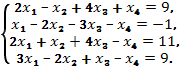
в) 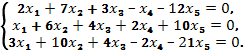
11. Найти фундаментальную систему решений для системы уравнений:
a) 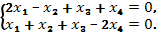
б) 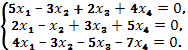
в) 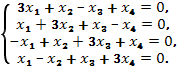
12. Вычислить:
а) 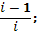 б)
б) 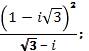 в)
в) 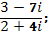 г)
г) 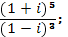 д)
д) 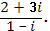
13. Представить в тригонометрической форме комплексные числа:
a) 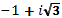 ; б)
; б) 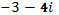 ; в)
; в)  ; г)
; г) 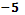 ; д); е)
; д); е) 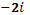 .
.
14. Вычислить, используя тригонометрическую форму комплексного числа:
а); б) 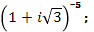 в)
в) 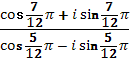 ; г)
; г) 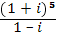 ;
;
д)  ; е)
; е) 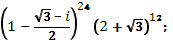
ж) 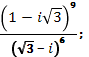 з)
з)  .
.
15. Найти все значения корней:
a) 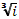 ; б)
; б) 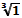 ; в)
; в) 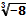 ; г)
; г) 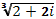 ; д)
; д) 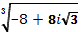 ; е)
; е) 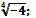 ж)
ж) 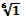 .
.
16. Решить уравнения:
а) 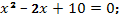
б) 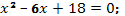
в) 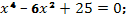
г) 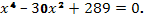
17. Определить острый угол между прямыми:
а) 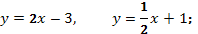
б)
в)
г) 
18. Определить расстояние между прямыми:
a) и
б) и 
19. Написать уравнение перпендикуляра к прямой, проходящей через две точки 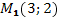 и
и 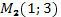 , восстановленного в середине отрезка
, восстановленного в середине отрезка 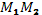 .
.
20. Написать уравнение прямой, проходящей через точку 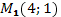 и точку
и точку 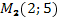 , и уравнение перпендикуляра к этой прямой в точке
, и уравнение перпендикуляра к этой прямой в точке 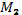 .
.
21. Написать уравнение прямой, проходящей через точки пересечения прямых:
 и
и  .
.
22. Написать уравнение перпендикуляра к прямой, проходящего через точку 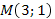 , и уравнение прямой, параллельной данной и тоже проходящей через точку
, и уравнение прямой, параллельной данной и тоже проходящей через точку 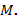
23. Построить кривые второго порядка:
а) 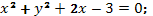
б) 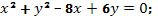
в) 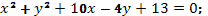
г) 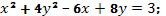
д) 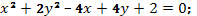
е) 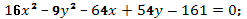
ж)
з) 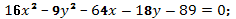
и) 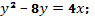
к) 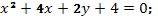
24. Составить уравнение плоскости, проходящей через:
a) точку 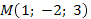 и перпендикулярной вектору
и перпендикулярной вектору 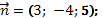
б) точки 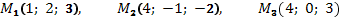 .
.
25. Составить уравнение прямой, проходящей через:
a) точку 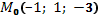 параллельно вектору
параллельно вектору 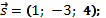
б) точки 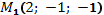 и
и 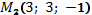 ;
;
в) точку 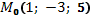 параллельно прямой
параллельно прямой 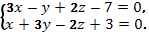
26. Найти угол между:
a) прямыми 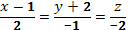 и
и 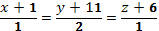 и выяснить, являются ли эти прямые пересекающимися или скрещивающимися;
и выяснить, являются ли эти прямые пересекающимися или скрещивающимися;
б) прямой 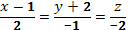 и плоскостью.
и плоскостью.
27. Выяснить, разлагается ли вектор 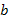 по системе векторов
по системе векторов 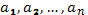 :
:
a) 
б) 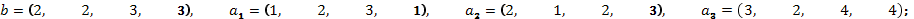
в) 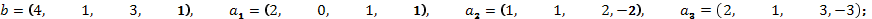
г) 
д) 
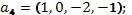
28. Выяснить, является ли данная система векторов линейно зависимой или линейно независимой:
a) 
б) 
в) 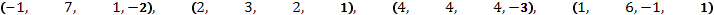 .
.
29. Найти базис системы векторов и векторы, не входящие в базис, разложить по базису:
a) 
б) 
в) 
г) 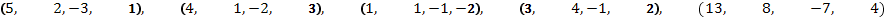 .
.
30. Найти базис и размерность линейной оболочки системы векторов:
a) 
б) 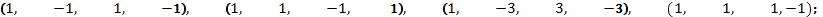
в) 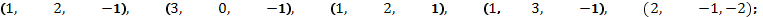
г) 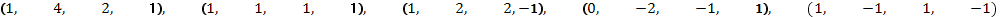 .
.
31. Доказать, что система матриц 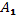 ,
, 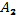 ,
, 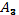 ,
, 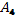 является базисом в пространстве матриц второго порядка, и найти в этом базисе координаты матрицы
является базисом в пространстве матриц второго порядка, и найти в этом базисе координаты матрицы 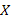 :
:
а) 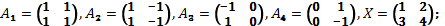
б) 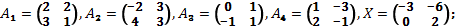
в) 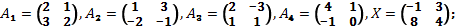
г) 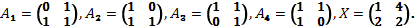
32. Применяя процесс ортогонализации, построить ортогональный базис линейной оболочки данной системы векторов:
а) 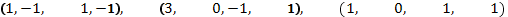
б) 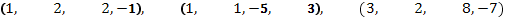
в) 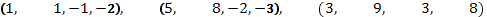
33. Выяснить, является ли преобразование 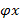 линейным, если вектор
линейным, если вектор 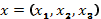 ?
?
а) 
б) 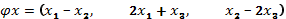
34. Найти собственные значения и собственные векторы матриц:
а) 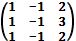 б)
б) 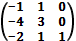 в)
в) 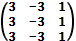 г)
г) 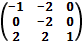
 2015-09-06
2015-09-06 512
512







