Доказательство.
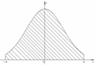
Пусть а < с < b и функция f (x) неотрицательна на [a, b]. Согласно геометрическому свойству определенного интеграла,
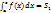 ,
, 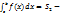 есть площади соответствующих криволинейных трапеций.
есть площади соответствующих криволинейных трапеций.
А площадь всей криволинейной трапеции - это 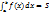
Тогда S = S 1 + S 2.
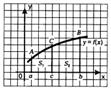
6. Если 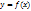 - нечетная функция, то
- нечетная функция, то 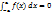
Доказательство (геометрически)
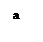
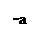

7. Если 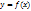 - четная функция, то
- четная функция, то
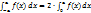
Доказательство (геометрически)
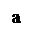
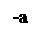
Приложения интеграла (Башмаков).
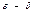 и на языке последова-тельностей.
и на языке последова-тельностей. 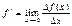 -предел разност отношения(вуз, а в школе в программах с 1968-1986)
2.Исторический(с 1986)
Не изучается понятие пре-дела, но символ
-предел разност отношения(вуз, а в школе в программах с 1968-1986)
2.Исторический(с 1986)
Не изучается понятие пре-дела, но символ 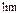 может использоваться как замена слову «стремле-ние». Данный подход реа-лизуется в школе. Этот подход назван истор, тк в мат-ке как известно,вначале были сформ-ны произ-ая и интеграл и позднее,обобщение этих понятий.
Введение понятия произ-водной:
1.Башмаков в определении производной использует знак
может использоваться как замена слову «стремле-ние». Данный подход реа-лизуется в школе. Этот подход назван истор, тк в мат-ке как известно,вначале были сформ-ны произ-ая и интеграл и позднее,обобщение этих понятий.
Введение понятия произ-водной:
1.Башмаков в определении производной использует знак 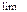 .
2.Колмогоров не исполь-зует этот знак.
Схеме введения и изучение производной.
1.Рассмотреть подводя-щую задачу, раскрыва-ющую физический смысл производной(нахождение мгновенной скорости свободного падения тела). 2.Сформулировать опр-ие понятия производной. 3.Конкретизировать поня-тие производной (примеры вычисления производной по определению физичес-кого смысла).
4.Рассмотреть приложе-ния производной.
Пример подводящей задачи.
Задача о нахождении мгновенной скорости.
Дано:S=S(t)-зависимость пути от времени.”?”Как охарактеризовать(найти)V в каждый данный момент времени.
Скорость в данный момент времени в физике наз мгновенной скоростью.Будем нах-ть ее с помощью понятия-средн. Скорость.
.
2.Колмогоров не исполь-зует этот знак.
Схеме введения и изучение производной.
1.Рассмотреть подводя-щую задачу, раскрыва-ющую физический смысл производной(нахождение мгновенной скорости свободного падения тела). 2.Сформулировать опр-ие понятия производной. 3.Конкретизировать поня-тие производной (примеры вычисления производной по определению физичес-кого смысла).
4.Рассмотреть приложе-ния производной.
Пример подводящей задачи.
Задача о нахождении мгновенной скорости.
Дано:S=S(t)-зависимость пути от времени.”?”Как охарактеризовать(найти)V в каждый данный момент времени.
Скорость в данный момент времени в физике наз мгновенной скоростью.Будем нах-ть ее с помощью понятия-средн. Скорость.
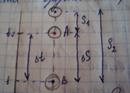 Зафиксир момент времени t0.Тело нах-ся в т.А Находим чему равна скорость тела в тВ. По рис. ∆S=S2-S1-расст которое прошло тело от Адо В.∆t-затрачен временной промежуток на этом участке.
Зафиксир момент времени t0.Тело нах-ся в т.А Находим чему равна скорость тела в тВ. По рис. ∆S=S2-S1-расст которое прошло тело от Адо В.∆t-затрачен временной промежуток на этом участке.
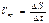 .Такая хар-ка будет оч грубой, тк Vср успела бы сильно уменьш.Будем
.Такая хар-ка будет оч грубой, тк Vср успела бы сильно уменьш.Будем 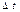 уменьшать,если взять
уменьшать,если взять 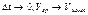 Мгновенная скорость- это число, к которому стремится отношение
Мгновенная скорость- это число, к которому стремится отношение 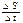 при стремлении
при стремлении 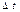 к 0.
Дано:y=f(x).найти:скорость изменения функции в нек-рой точке.
Сравнить скорости изменения фун по графику.
к 0.
Дано:y=f(x).найти:скорость изменения функции в нек-рой точке.
Сравнить скорости изменения фун по графику.
 1)выберем приращение ∆х.
2)найдем f(х0+∆х)
3)найдем приращение f= f(х0+∆х)-f(x0)
4)найдем средн скорость изменения функции ∆f/∆x
5)
1)выберем приращение ∆х.
2)найдем f(х0+∆х)
3)найдем приращение f= f(х0+∆х)-f(x0)
4)найдем средн скорость изменения функции ∆f/∆x
5) 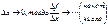 называемое производной функции в точке.
Опред: Производной функции f в точке x0 называется число, к которому стремится разностное отношение
называемое производной функции в точке.
Опред: Производной функции f в точке x0 называется число, к которому стремится разностное отношение
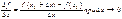 Можно предложить уч-мся и другие привод задачи(колм,мордк).
Алгоритм нахождения производн:
1)х0 придаем приращ ∆х
2)находим ∆f(изменен функ)
3)нах ∆f/∆x(сред скорость)
4)берем ∆х—0 и нах число, к котор стрем ∆f/∆x.
Пример:найдем произв функ y=x^3 в т х0.
1)х0 задаем приращ ∆х
2)∆f=(х0+∆х)^3-х0^3= х0^3+3х0^2∆х+3x0(∆х)^2+∆х^3-x0^3=3х0^2∆х+3x0(∆х)^2+∆х^3
3) ∆f/∆x=подставл
4)3х0^2постоянно, 3х0, ∆х—0 при ∆х---0 (∆х)^2—0 при ∆х—0,
) ∆f/∆x---3х0^2 при ∆х—0.
Если к гр функ y=f(x) в т.с абсциссой х=а можно провести касат непаралл оси Y,то f//(а) выраж углов коэф касат.
равен
Можно предложить уч-мся и другие привод задачи(колм,мордк).
Алгоритм нахождения производн:
1)х0 придаем приращ ∆х
2)находим ∆f(изменен функ)
3)нах ∆f/∆x(сред скорость)
4)берем ∆х—0 и нах число, к котор стрем ∆f/∆x.
Пример:найдем произв функ y=x^3 в т х0.
1)х0 задаем приращ ∆х
2)∆f=(х0+∆х)^3-х0^3= х0^3+3х0^2∆х+3x0(∆х)^2+∆х^3-x0^3=3х0^2∆х+3x0(∆х)^2+∆х^3
3) ∆f/∆x=подставл
4)3х0^2постоянно, 3х0, ∆х—0 при ∆х---0 (∆х)^2—0 при ∆х—0,
) ∆f/∆x---3х0^2 при ∆х—0.
Если к гр функ y=f(x) в т.с абсциссой х=а можно провести касат непаралл оси Y,то f//(а) выраж углов коэф касат.
равен 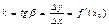 .
Физич:если s(t)-закон прямол движения тела, то производ выражает мгновен скорость в момент времени t.
Применение производной к исследованию функции. Схема:
1.D(f)
2.Исследование на четность. 3.Вычислить производную. 4.Критические точки(
.
Физич:если s(t)-закон прямол движения тела, то производ выражает мгновен скорость в момент времени t.
Применение производной к исследованию функции. Схема:
1.D(f)
2.Исследование на четность. 3.Вычислить производную. 4.Критические точки(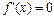 ). 5.Промежутки монотонности (
). 5.Промежутки монотонности (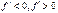 )
6.Точки экстремума
7.График.
Приложения производной:
1.Уравнение касательной:
)
6.Точки экстремума
7.График.
Приложения производной:
1.Уравнение касательной: 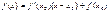 2.Нахождение числа корней уравнения.
3.Приближенные вычисления:
2.Нахождение числа корней уравнения.
3.Приближенные вычисления: 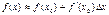 Следует разделять понятия: производная функции в точке- это число, а производная функции- это некоторая функция, которая обозначается
Следует разделять понятия: производная функции в точке- это число, а производная функции- это некоторая функция, которая обозначается 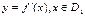 , D1- мн-во точек, где функция дифференцируема.
, D1- мн-во точек, где функция дифференцируема.
 ] синус которого равен а.
(
] синус которого равен а.
(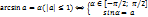 )
б)) арккосинусом числа а(|a|≤1) называется такое число из промежутка [0;
)
б)) арккосинусом числа а(|a|≤1) называется такое число из промежутка [0;  ] косинус которого равен а.
(arccos a=α(|a|≤1)⟺
] косинус которого равен а.
(arccos a=α(|a|≤1)⟺ 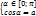 )
в) арктангенсом числа а(|a|≤1) называется такое число из промежутка (-π/2; π/2) тангенс которого равен а.
г) арккотангенсом числа а(|a|≤1) называется такое число из промежутка (0;π) котангенс которого равен а.
1)Простейшие тригоном. уравнения- это уравнения вида:
sinx=a; cosx=a; tgx=a; ctgx=a.
где х- переменная, а- любое действительное число.
Способы решения: простейшие триг.уравнения решаются с помощью формул, а так же с помощью ед.окружности.
Общая формула:
)
в) арктангенсом числа а(|a|≤1) называется такое число из промежутка (-π/2; π/2) тангенс которого равен а.
г) арккотангенсом числа а(|a|≤1) называется такое число из промежутка (0;π) котангенс которого равен а.
1)Простейшие тригоном. уравнения- это уравнения вида:
sinx=a; cosx=a; tgx=a; ctgx=a.
где х- переменная, а- любое действительное число.
Способы решения: простейшие триг.уравнения решаются с помощью формул, а так же с помощью ед.окружности.
Общая формула: 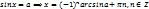 Частные формулы: sinx=0⟹х= πn
sinx=1⟹х=
Частные формулы: sinx=0⟹х= πn
sinx=1⟹х= 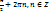 cosx=-1⟹х= -π/2+2πn, n∈Z.
Общая формула:
cosx=a⟹ x=±arccosa+2πn,n∈Z
cosx=0⟹х= π/2+ πn, n∈Z
cosx=1⟹х= 2πn,n∈Z
cosx=-1⟹х= π+2πn, n∈Z.
Общая формула:
tgx=a⟹ x=arctga+πn, n∈Z
ctgx=a⟹ x=arcctga+πn, n∈Z.
2) Триг. уравнения сводимые к квадратному(метод решения- введение новой переменной)
cosx=-1⟹х= -π/2+2πn, n∈Z.
Общая формула:
cosx=a⟹ x=±arccosa+2πn,n∈Z
cosx=0⟹х= π/2+ πn, n∈Z
cosx=1⟹х= 2πn,n∈Z
cosx=-1⟹х= π+2πn, n∈Z.
Общая формула:
tgx=a⟹ x=arctga+πn, n∈Z
ctgx=a⟹ x=arcctga+πn, n∈Z.
2) Триг. уравнения сводимые к квадратному(метод решения- введение новой переменной)
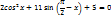
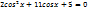
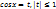
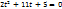 3)Однородные уравнения а)1-ой степени: asin(x)+bcos(x)=0,б) 2-ой степени:asin2(x)+bsin(x)cos(x)+ cos2(x)=0.
Метод решения: 1-ой степени: деление на cosx≠0 (Проверяем не потеряны ли корни: пусть cosx=0, подставим в уравнение:
3)Однородные уравнения а)1-ой степени: asin(x)+bcos(x)=0,б) 2-ой степени:asin2(x)+bsin(x)cos(x)+ cos2(x)=0.
Метод решения: 1-ой степени: деление на cosx≠0 (Проверяем не потеряны ли корни: пусть cosx=0, подставим в уравнение:
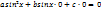 ⟹sinx=0
А это не возможно в силу основного триг.тождества
⟹sinx=0
А это не возможно в силу основного триг.тождества 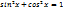 б) 2-ой степени: делим на
б) 2-ой степени: делим на 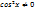 , т.к. в противном случае sinx=0, что невозможно.
, т.к. в противном случае sinx=0, что невозможно.
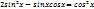 |:
|: 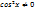
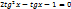 , tgx=a
, tgx=a
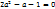 в) уравнения сводимые к однородному
asin(x)+bcos(x)=d, где d=d∙1=d∙(
в) уравнения сводимые к однородному
asin(x)+bcos(x)=d, где d=d∙1=d∙(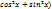 4) Уравнения решаемые разложением на множители
4) Уравнения решаемые разложением на множители
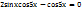 cos5x(2sinx-1)=0
cos5x=0 или 2sinx-1=0
5x= π/2+ πn, n∈Z sinx=1/2
x= π/10+ πn/5 x=
cos5x(2sinx-1)=0
cos5x=0 или 2sinx-1=0
5x= π/2+ πn, n∈Z sinx=1/2
x= π/10+ πn/5 x= 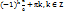 5)Уравнения вида:asin(x)+bcos(x)=c
3 метода решения:
· Введение вспомогательного угла
· Метод универсальной подстановки
5)Уравнения вида:asin(x)+bcos(x)=c
3 метода решения:
· Введение вспомогательного угла
· Метод универсальной подстановки 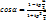
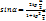 · Сведение к однородному
· Сведение к однородному
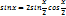
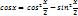 c=c∙1=c∙(
c=c∙1=c∙(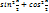 )
Рассмотрим решение уравнений методом вспомогательного угла:
asin(x)+bcos(x)=c, a,b,c≠0
)
Рассмотрим решение уравнений методом вспомогательного угла:
asin(x)+bcos(x)=c, a,b,c≠0
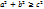 условие уравнения
условие уравнения
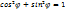 , cos φ=a, sin φ=b⟹
, cos φ=a, sin φ=b⟹ 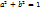
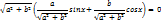
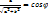 ;
; 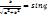
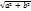 (cosφ sinx+ sinφ cosx)=c
(cosφ sinx+ sinφ cosx)=c
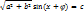
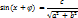
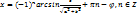 ,
,
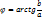
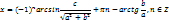 6) Уравнения решаемые с использованием различных тригонометрических формул(понижение степени, преобразование суммы триг.функций в произведение)
6) Уравнения решаемые с использованием различных тригонометрических формул(понижение степени, преобразование суммы триг.функций в произведение)
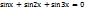 (sinx+ sin3x) + sin2x =0
(sinx+ sin3x) + sin2x =0
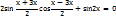 2sin2x∙cos(-x)+sin2x=0
sin2x(2cosx+1)=0
7) Уравнения решаемые оценкой левой и правой части
2sin2x∙cos(-x)+sin2x=0
sin2x(2cosx+1)=0
7) Уравнения решаемые оценкой левой и правой части
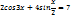 Замечаем, что |cos3x|≤1, |sin
Замечаем, что |cos3x|≤1, |sin  |≤1⟹ |2cos3x+4sin
|≤1⟹ |2cos3x+4sin  |≤6⟹ уравнение не имеет решений.
Методы решения триг.уравнений:
ü Введение новой пременной
ü Разложение на множители
ü Метод введения вспомогательного угла
ü Метод универсальной подстановки
ü Метод деления левой и правой части
ü Метод оценки левой и правой части
Виды: однородные, приводимые к квадратному, и asinx+bcosx=c
|≤6⟹ уравнение не имеет решений.
Методы решения триг.уравнений:
ü Введение новой пременной
ü Разложение на множители
ü Метод введения вспомогательного угла
ü Метод универсальной подстановки
ü Метод деления левой и правой части
ü Метод оценки левой и правой части
Виды: однородные, приводимые к квадратному, и asinx+bcosx=c
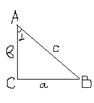
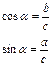 (косинус угла
(косинус угла 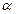 зависит от величины угла
зависит от величины угла 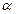 , а не от размеров треуг.).
Т.о, триг фун-ия определяется от углового аргумента
, а не от размеров треуг.).
Т.о, триг фун-ия определяется от углового аргумента 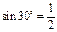 (300 –угол, ½ - число)
Такие фун-ии неудобны для исследования, т.к. учащиеся умеют исследовать фун-ии числового аргумента.
4) Введение тригоном-й функции числового аргумента:
Прежде всего надо повторить понятие «ед. окружность»
Рассмотрим возможные введения триг-ой функции числового аргумента:
(300 –угол, ½ - число)
Такие фун-ии неудобны для исследования, т.к. учащиеся умеют исследовать фун-ии числового аргумента.
4) Введение тригоном-й функции числового аргумента:
Прежде всего надо повторить понятие «ед. окружность»
Рассмотрим возможные введения триг-ой функции числового аргумента:
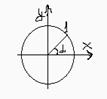 1.Делается переход от измерения углов в градусной мере к радианной. Радианную меру считают числом(Колмогоров).
«sin(x)» означает sin угла в x радиан.
2.Обосновывается, что радианную меру угла можно считать числом в ед. окружности.
Угол в 1 рад – центральный угол в окружности который опирается на длину дуги равную радиусу окружности.
2.Определяем синус угла в ед. окр.: пусть т.А имеет корд (х0,у0), синусом числа
1.Делается переход от измерения углов в градусной мере к радианной. Радианную меру считают числом(Колмогоров).
«sin(x)» означает sin угла в x радиан.
2.Обосновывается, что радианную меру угла можно считать числом в ед. окружности.
Угол в 1 рад – центральный угол в окружности который опирается на длину дуги равную радиусу окружности.
2.Определяем синус угла в ед. окр.: пусть т.А имеет корд (х0,у0), синусом числа 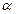 в единичной окружности наз. ордината точки единичной окружности, изображающей угол в
в единичной окружности наз. ордината точки единичной окружности, изображающей угол в 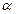 радиан. sin
радиан. sin 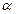 =у0
3.Строим зависимость: каждому числу Х соответствует точка ед. окр. С определённой ординатой, т.е. sin(x) => имеем зависимость х -> sin(x).
4.Опр: Числовая функция, заданная формулой y = sin(x) наз. синусом.
5. Строится график функции y = sin(x). 1способ: с помощью ед. окр. (Колмаг, Башм, Алимов)
2способ: по таблице значений синусов для некот-х чисел
(Мордкович)
Обратить внимание при первом построении графика ф-ии:
1. Использ некот св-ва ф-ии (ооф,озф,чет,нечёт, известные формулы)
2. Обосновать выбор ед отрезка в системе корд 1ед = 2 клетки (для удобства)
3. Показать нахождение точек на оси ОХ: П/6, П/3, П/4, П, 2П. П≈6 клеток.
5)Все тригонометрические функции обладают свойством периодичности.
Опред: Функцию f наз. периодической с периодом
=у0
3.Строим зависимость: каждому числу Х соответствует точка ед. окр. С определённой ординатой, т.е. sin(x) => имеем зависимость х -> sin(x).
4.Опр: Числовая функция, заданная формулой y = sin(x) наз. синусом.
5. Строится график функции y = sin(x). 1способ: с помощью ед. окр. (Колмаг, Башм, Алимов)
2способ: по таблице значений синусов для некот-х чисел
(Мордкович)
Обратить внимание при первом построении графика ф-ии:
1. Использ некот св-ва ф-ии (ооф,озф,чет,нечёт, известные формулы)
2. Обосновать выбор ед отрезка в системе корд 1ед = 2 клетки (для удобства)
3. Показать нахождение точек на оси ОХ: П/6, П/3, П/4, П, 2П. П≈6 клеток.
5)Все тригонометрические функции обладают свойством периодичности.
Опред: Функцию f наз. периодической с периодом 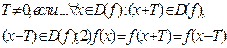 2
2 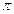 - наименьший положительный период для y = sin(x), y=cos(x),
- наименьший положительный период для y = sin(x), y=cos(x), 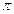 - наименьший положительный период для y=tg(x), y=ctg(x).
Если функция f периодическая и имеет период Т0, то функция A
- наименьший положительный период для y=tg(x), y=ctg(x).
Если функция f периодическая и имеет период Т0, то функция A  f(kx+b), где A,k,b- постоянные и
f(kx+b), где A,k,b- постоянные и 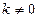 , также периодична и ее период =
, также периодична и ее период = 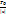 6) Монотонность: очень важно, чтобы учащиеся запомнили промежутки монотонности триг функций, близких к нулю:
1.
6) Монотонность: очень важно, чтобы учащиеся запомнили промежутки монотонности триг функций, близких к нулю:
1. 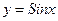 возрост. на промеж.
возрост. на промеж. 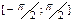 2.
2. 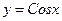 убыв. на пром.
убыв. на пром. 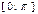 3.
3. 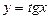 возр. на интерв.
возр. на интерв. 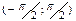 4.
4. 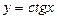 убыв. на интерв.
убыв. на интерв. 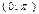 .
7) Исследование тригонометрической функции на примере:
.
7) Исследование тригонометрической функции на примере:
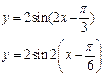 График…
1.D(f)=R; E(f)=[-2;2];
2. Функция общего вида.;
3. Период
График…
1.D(f)=R; E(f)=[-2;2];
2. Функция общего вида.;
3. Период 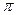 4.Нули функции:
4.Нули функции:
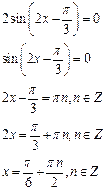 5.Точки пересечения с (Ох):
5.Точки пересечения с (Ох): 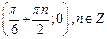 ;
с (Оу):
;
с (Оу): 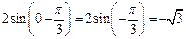
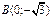 6. у возр на
6. у возр на 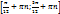 , у убыв на
, у убыв на 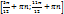 7. Промежутки знакопостоянства:
У>0 при х принадл
7. Промежутки знакопостоянства:
У>0 при х принадл 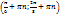 У<0 при х принадл
У<0 при х принадл 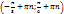 , n принадл Z
8. Точки экстремума:
Хмах=
, n принадл Z
8. Точки экстремума:
Хмах= 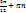 ; хмин=
; хмин= 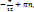 n принадл Z
9. Экстремумы: умах=2, умин=-2
8. Наиб и наим знач: унаиб= 2, унаим=-2
n принадл Z
9. Экстремумы: умах=2, умин=-2
8. Наиб и наим знач: унаиб= 2, унаим=-2
 2015-10-16
2015-10-16 407
407






