Сила тяжіння (гравітації) 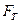 до Землі кожного тіла, що знаходиться в полі земного тяжіння, спрямована до центру Землі і дорівнює:
до Землі кожного тіла, що знаходиться в полі земного тяжіння, спрямована до центру Землі і дорівнює:
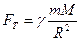 , (12.1)
, (12.1)
де 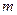 ,
, 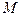 – маси відповідно тіла і Землі;
– маси відповідно тіла і Землі; 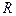 – відстань від тіла до центра Землі.
– відстань від тіла до центра Землі.
Вона зумовлює добове обертання тіла разом із Землею, а також спричинює тиск на опору.
Сила, з якою тіло діє на горизонтальну опору або на підвіс внаслідок притягання до Землі, називається вагою тіла 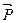 .
.
В усіх інерційних системах відліку вага тіла однакова і чисельно дорівнює силі тяжіння (точкою прикладання сили тяжіння є центр мас тіла, точкою прикладання ваги – опора або підвіс):
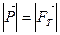 (12.2)
(12.2)
Рух тіла під дією сили тяжіння 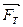 називається вільним падінням, а прискорення
називається вільним падінням, а прискорення 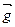 , якого набуває при цьому тіло, прискоренням вільного падіння або прискоренням сили тяжіння. За другим законом Ньютона
, якого набуває при цьому тіло, прискоренням вільного падіння або прискоренням сили тяжіння. За другим законом Ньютона
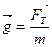 . (12.3)
. (12.3)
Прискорення вільного падіння експериментально можна визначити за допомогою математичного маятника – матеріальної точки, підвішеної на невагомій нерозтяжній нитці.
Моделлю математичного маятника може бути кулька, підвішена на довгій (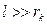 ) нитці, що мало розтягується, масою якої можна знехтувати порівняно з масою кульки (
) нитці, що мало розтягується, масою якої можна знехтувати порівняно з масою кульки (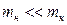 ).
).
Коливання математичного маятника відбуваються під дією сили тяжіння. Коли маятник знаходиться в положенні рівноваги, сила тяжіння врівноважується силою пружності нитки. Якщо ж маятник відхилити на кут 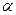 (рис.12.1), то сила пружності нитки буде зрівноважувати тільки одну складову сили тяжіння
(рис.12.1), то сила пружності нитки буде зрівноважувати тільки одну складову сили тяжіння 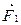 , напрямлену вздовж нитки. Друга складова
, напрямлену вздовж нитки. Друга складова 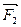 , спрямована до положення рівноваги, залишається неврівноваженою. Як видно із рис.12.1,
, спрямована до положення рівноваги, залишається неврівноваженою. Як видно із рис.12.1, 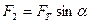 . При малих кутах відхилення (10…15
. При малих кутах відхилення (10…15 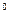 )
) 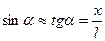 , та з урахуванням (12.2):
, та з урахуванням (12.2):
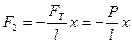 , (12.4)
, (12.4)
де 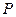 – вага кульки; l – довжина нитки; х – зміщення від положення рівноваги. Знак «-» в (12.4) вказує на те, що сила
– вага кульки; l – довжина нитки; х – зміщення від положення рівноваги. Знак «-» в (12.4) вказує на те, що сила 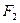 завжди напрямлена протилежно зміщенню х, тобто є повертаючою.
завжди напрямлена протилежно зміщенню х, тобто є повертаючою.
З (12.4) видно, що повертаюча сила 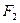 пропорційна зміщенню х. Під дією сили, пропорційної зміщенню і спрямованої до положення рівноваги, виникають гармонічні коливання, тобто коливання, які описуються рівнянням
пропорційна зміщенню х. Під дією сили, пропорційної зміщенню і спрямованої до положення рівноваги, виникають гармонічні коливання, тобто коливання, які описуються рівнянням
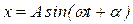 , (12.5)
, (12.5)
де х – величина зміщення матеріальної точки від положення рівноваги (в даний момент часу); А – амплітуда коливань (найбільше відхилення матеріальної точки від положення рівноваги); 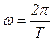 – циклічна частота (число коливань за час 2
– циклічна частота (число коливань за час 2 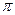 секунд), Т – період коливань, t – час,
секунд), Т – період коливань, t – час, 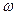 t+
t+ 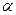 – фаза коливання,
– фаза коливання, 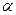 – початкова фаза.
– початкова фаза.
Запишемо рівняння руху матеріальної точки, викликаного повертаючою силою 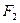 :
:
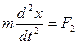 . (12.6)
. (12.6)
Підставивши у (12.6) 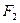 із (12.4), отримаємо
із (12.4), отримаємо
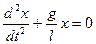 ;
;
(12.7)
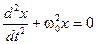 .
.
Співвідношення (12.7) є диференціальним рівнянням гармонічного коливання математичного маятника.
З урахуванням того що, 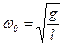 – циклічна частота власних коливань математичного маятника, період його коливань
– циклічна частота власних коливань математичного маятника, період його коливань
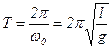 . (12.8)
. (12.8)
Із (12.8) можна визначити прискорення вільного падіння g через довжину математичного маятника l та період його коливань 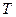 :
:
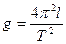 . (12.9)
. (12.9)
 2015-10-16
2015-10-16 281
281








